前言

先講kernel method，Neural Network之後再講。

主題

為什麼要先講kernel method呢?因為，從Perceptron講到SVM和Kernel關聯性很高，也有很多角度可以切入。

Kernel Method

從前面Perceptron來延伸兩項問題:

1. 最佳解是否唯一?
   從下圖來看，我們可以發現想把資料分成兩部分，可以有無限多種的直線成立。
   那這些解之中哪條才是最好的呢?要如何才能得到最好的解呢?
   從機器學習的目的來看，我們會希望得到的模型能夠對未知的資料進行預測。因此，假設未知的資料理論上也會跟附近的已知資料是相同的Label，那麼考慮一條與兩邊資料距離最遠的線，或許能夠在對未知資料的預測上，取得不錯的成果。而這就是SVM(Support Vector Machine)的簡單概念。
   要如何確保距離會是最大呢?這邊的推導牽涉到線性規劃LP(Linear Programming)的方法。簡單給大方向，可以從國高中學過，點到線段、點到平面距離的公式去切入。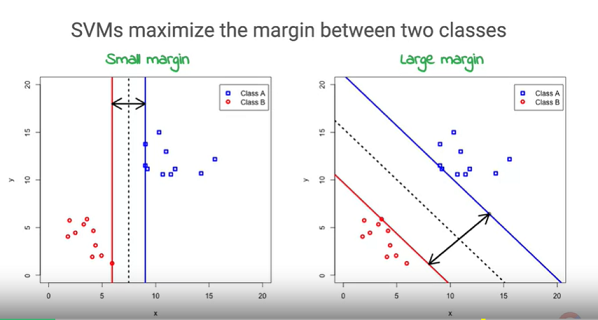
   

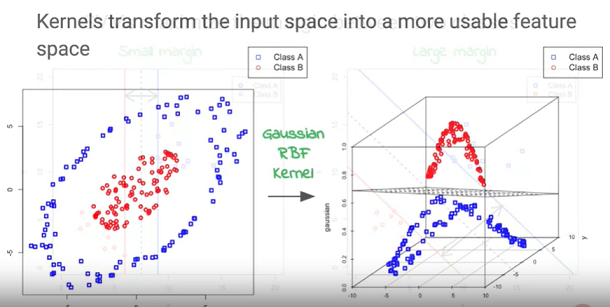
2. 如果不是線性可分該怎麼辦?
   此問題最簡單而暴力的解法，就是把資料投影到更高的維度中，想辦法讓這些資料在高維度的空間中是能夠線性可分的。然而，這樣產生出另一項問題，該怎麼找出"把資料投影到高維度的合適函數"?找出此項函數反而變成case by case更麻煩的工作。
   所幸，後來從dual problem中，發現投影到高維度後，資料間會再取內積進行運算。因此，事實上只要確保高維度中資料之間向量內積的關係就好了，透過公式的推導得到利用Kernel function，取代先將資料投影到高維度再進行內積的過程，而是直接使用原始資料通過Kernel，就能獲得資料間在高維度中向量內積的關係，再以此去找出合適的線性分類函數。