嗨大家好，今天來跟大家討論圖論問題(Graph Theory)中常見的最短路徑演算法：Floyd-Warshall 演算法以及 Bellman-Ford 演算法。

最短路徑題目是這樣的，通常有分成三個層次。

• 單一點對最短路徑：給定 s, t，計算 s 到 t 的最短路徑長度。
• 單一源點最短路徑（Single Source Shortest Path, SSSP）：給定源點 s，計算該點到所有點的最短路徑長度。
• 所有點對最短路徑（All Pair Shortest Path, APSP）：給定整張圖 G，計算任意兩點之間的最短距離。

而常見的演算法都是透過一種叫做「鬆弛」的動作來更新點對之間的距離的！

鬆弛 Relaxation

其實就是說「嘿，我找到另一條可能的路徑，你要不要考慮看看」這種感覺。假設你一開始已經有記錄下 u, v 之間的距離了 d(u, v)，那如果你發現了另一個點 x，使得 d(u, x) + d(x, v) < d(u, v)，那你當然可以把 d(u, v) 換成更小的距離！

這個鬆弛操作，就可以當作動態規劃的其中一個遞迴關係囉！只不過，遞迴關係要能夠變成動態規劃演算法，必須要讓依賴的子問題變小才行。所以我們得找一個「有嚴格變小」的關係量，才能夠讓動態規劃算出來是對的。

Path-Doubling Method

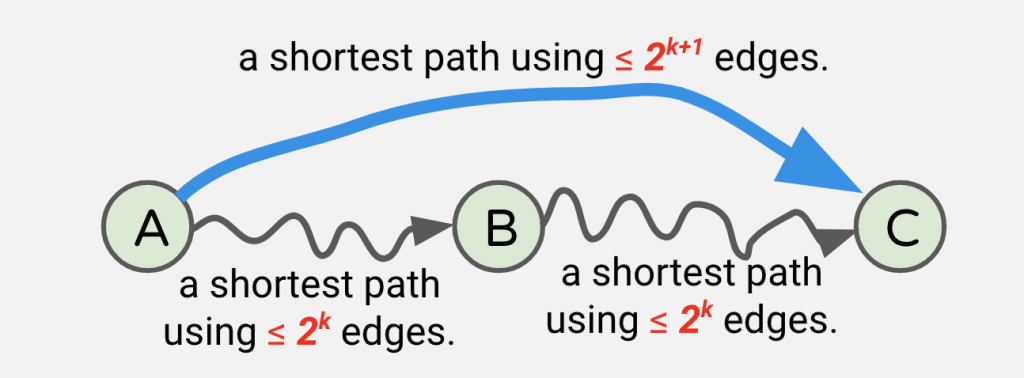
這個方法是每次擴充 d(2^k, u, v)：定義 u 到 v 使用不超過 2^k 條邊的最短路徑。因此我們可以得到以下遞迴式：

對於任意點對 u, v 來說，某條 u, v 之間的最短路徑只需要至多 n-1 條邊，因此我們可以讓 k 的最大值取到 log(n) 就好了（以 2 為底）。

Floyd-Warshall 演算法 (APSP)

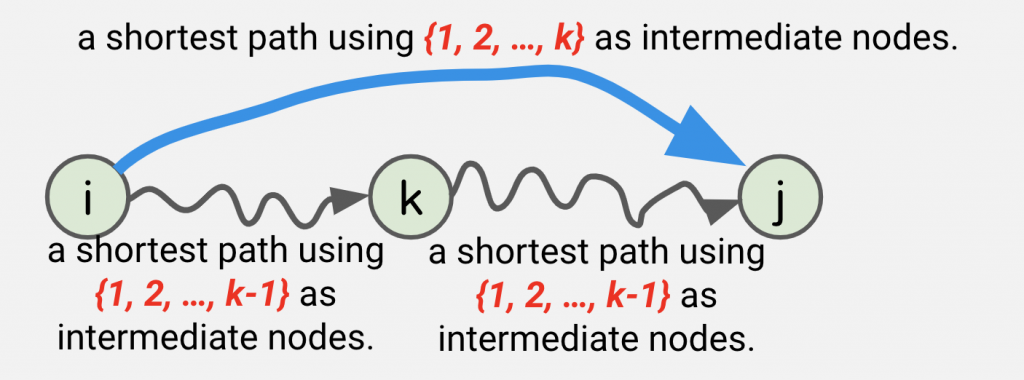
這個演算法只是更換了上面的定義：改成 d(k, u, v)：定義 u 到 v 僅使用編號 1~k 的中繼點所形成的最短路徑長度。因為某條 u, v 之間的最短路徑上頭的點，一定不會重複，因此考慮 k 到底有沒有出現在 u, v 的最短路徑中間，就變成了一個可以拿來建構動態規劃的狀態轉移了。我們可以得到以下遞迴式子：

寫成迴圈只要 n^3 時間呢~

Bellman-Ford 演算法 (SSSP)

這個演算法只需要關心單一源頭，因此我們不太能用「路徑剖半」的方式處理狀態轉移，因為可能會多出其他「出發點不同」的子問題。也因為不能用出發點不同的子問題，所以我們可以只考慮「最後一條邊」，也就是說 dp(k, v) 的定義為從源點 s 到點 v 經過至多 k 條邊的最短路徑長度。

轉移可以寫成：

時間複雜度是 O(n*m)。