在迴歸分析中，欲預測的資料是連續的數字，因此用圖形呈現的話可能會類似於一條線如下圖，而在這種狀況下，如果要得知預測結果與期望值的誤差是多少，則可以用均方誤差(Mean-Square Error, MSE)來計算。

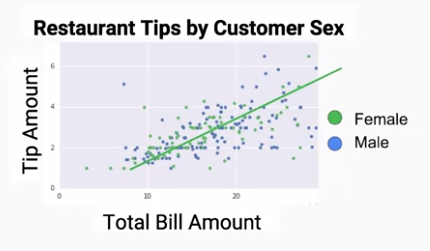
但若欲預測的標籤並非連續數字，需要以分類來進行演算，同樣以上圖為例，我們可以看到圖形中的女性及男性分布的十分分散，無法明確地以一個幾何圖形來表示兩個標籤的分布，而在這種非線性的狀況下，如果要得知預測結果與期望值的誤差是多少，則可以用交叉熵 (Cross-entropy) 來計算。

了解分類及迴歸分析後，接下來就是講古時間囉，首先最早出現的演算法線性回歸 (Linear Regression) ，一開始的用途是來預測星球移動，以及依碗豆的特徵來推測碗豆會有多大顆，法蘭西斯·高爾頓爵士 (Sir Francis Galton) 是寫演化論很有名那個達爾文的表弟，他也是線性回歸的先驅，他一開始是在研究各種物種的親代與子代間各項特徵是不是有關係，並畫出了史上第一個折線圖，當時是一個電腦科學尚未普及的時代，他並不知道接下來有許許多多的電腦科學家將以此為基礎，打造出無限的可能性。

在預測一件事時，我們可能會透過資料的多個特徵來進行預測，而每個特徵可能會對於結果的影響有不同的影響程度，因此我們會對於個特徵加上一個權重，至於權重要如何決定損失函數 (Loss function) 來評估。

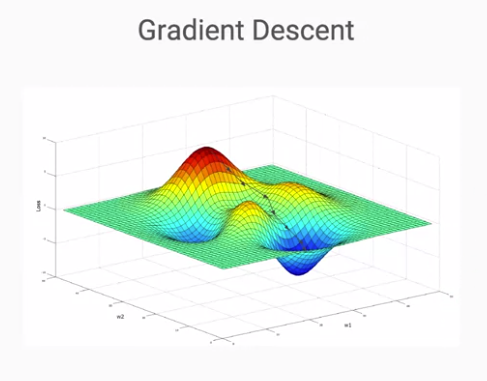
在處理真實世界的資料時，我們往往會發現真實資料的複雜度比起實驗資料來的多許多，當畫成圖的時候會變得像是地球表面的3D圖，其中有比較凸起的山丘，也有低下去的山谷，在這種狀況下就可以裡用梯度下降法 (Gradient Descent) 來計算誤差，進而推論出各特徵的權重為何，想像我們現在在未知的狀況下，想要找到一個最低的山谷有多深，因此我們必須適當的踏出每一步的距離，步伐太小的話會多走很多路，浪費很多體力，但步伐太大的話又可能會導致忽略了最低的那個點，而如何找到那個適當的步伐大小，就是梯度下降法可以解決的問題。