RSA

• 由Ron Rivest、Adi Shamir 和 Leonard Adleman 提出
• 安全基礎
  • 質因數分解問題

基本數學

Euler φ function

• 又名尤拉函數、歐拉函數

• φ(n)：比 n 小且與 n 互質的數

φ(4) = 2
因為比4小且互質的數有 1 和 3

• 性質
  • 如果 n 是質數：φ(n) = n - 1
  • 如果 p 、 q 是質數：φ(pq) = φ(p) * φ(q) = (p-1)(q-1)
  • 如果 p 是質數：φ(p^k) = p^k - p^(K-1)

mod ; 模運算

7 / 4 = 1 ... 3

7 mod 4 = 3
    
4 稱為「模數」

• 性質

  • (a mod p) ∗ (b mod p) = (a ∗ b) mod p

  (5 mod 3) ∗ (7 mod 3) = (5 ∗ 7) mod 3 = 2
  

• 除法

  • 模運算中，看到除法要轉成乘法，除數要改成在該模數下的模反元素

Example：

16 / 2 mod 3 = 2

可以看成是 16 乘以 2 在模數 3 的模反元素

16 ∗ invert(2,3) mod 3

等於

16 * 2 mod 3 = 2

這個 invert 指 2 在模數 3 下的模反元素

mod inverse ; 模反元素

• 乘法反元素: 兩個數字相乘 = 1

  Example：3 和 1/3 互為對方的乘法反元素
  

• 模反元素: 兩個數字相乘後，除以模數的餘數 = 1

  • 若 d 是 e 在模數是 $φ$(n) 下的模反元素
    • e * d ≡ 1 (mod $φ$(n))
    • e * d % $φ$(n) = 1

      Example：e = 3 、 d = 5 、 $φ$(n) = 7
      

• 求法

  • 暴力窮舉
  • 費馬小定理
  • 擴展歐基里德演算法

• Python

from Crypto.Util.number import inverse 
print(inverse(3, 7)) # 5

import gmpy2 print(gmpy2.invert(3, 7)) # 5

基本概念

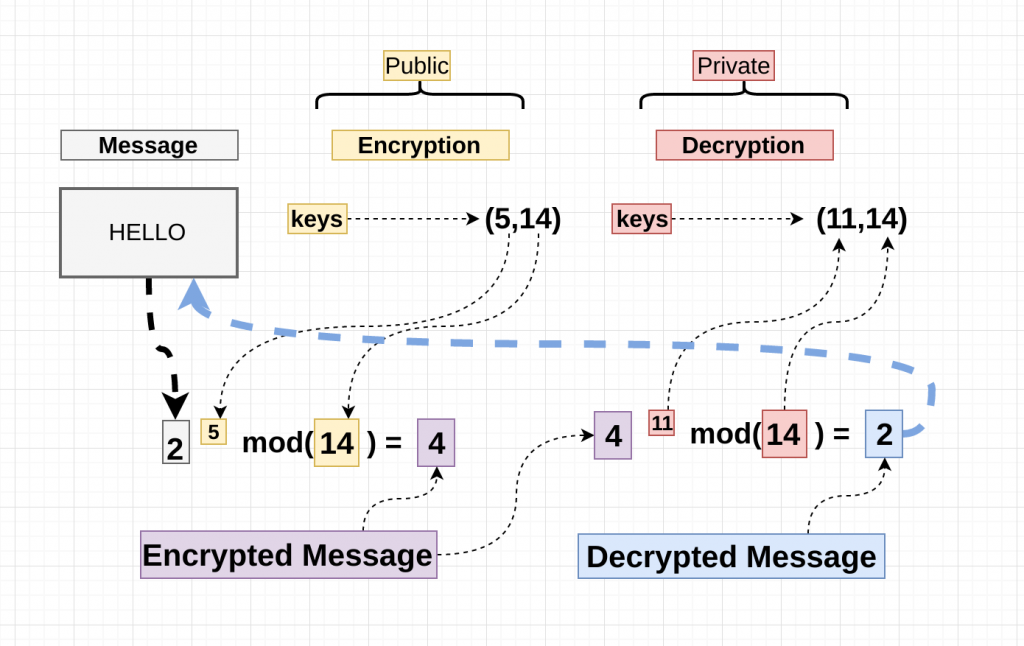
• 金鑰生成

  • 選兩個質數 p、q

    • n = p * q
    • φ(n) = (p-1) * (q-1)

  • 隨便找個數字 e

    • 小於 φ(n)
    • gcd(e, φ(n)) = 1

  • 透過 e 與 φ(n) 計算 d

    • e * d mod φ(n) = 1 (即 d 為 e 在 mod φ(n) 下之乘法反元素)

  • Public Key = (e, n)

  • Private Key = d

• 加密：C(密文) = P(明文)^e^ mod n

C = pow(M,e,N)

• 解密：P(明文) = C(密文)^d^ mod n

M = pow(C,d,N)

明文必定小於 n

• 舉例

  • P(明文)=2

  • 已知 n = 33、e = 13 ，則

    • p = 3 、 q = 11
    • φ(n) = (3-1)x(11-1) = 20
    • d = 17
      • e * d mod φ(n) = 1
        13 * d mod 20 = 1
        當 (13 * n - 1) % 20 == 0
        d = n

  • 加密

    • C = 2^13^ mod 33 = 8

  • 解密

    • P = 8^17^ mod 33 = 2