再校正完一組深度相機的時候，
我們要開始對特徵點進行三角測量，
可以跟單目相機的情況一樣假設左邊的相機沒有旋轉位移，
透過校正出來的R|t來推算出右邊相機的投影矩陣，
也可以讀取直接校正出來的外部參數P1、P2，左右相機的投影矩陣來做三角測量，
有了左右相機的投影矩陣以及特徵點匹配的結果，
我們就能做三角測量還原特徵點的3D座標。

而在雙目相機的情況下我們能做的事情更多了，
我們可以透過兩個相機之間的空間關係，
來過濾我們的特徵點匹配，而不是僅透過描述符的差異來過濾匹配的結果。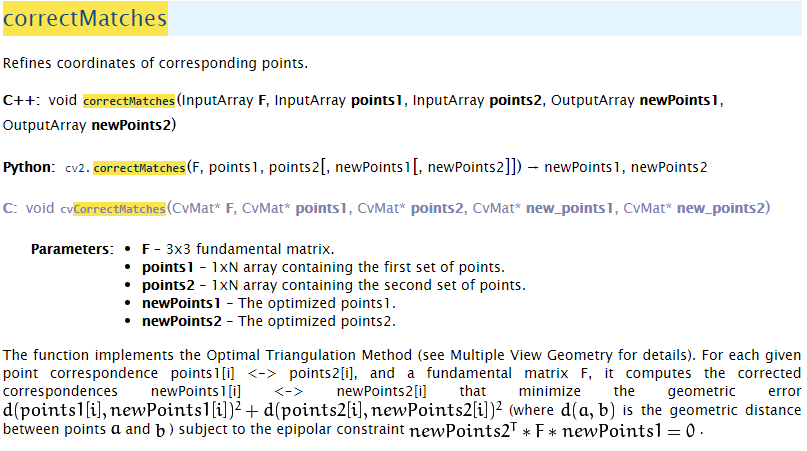

我們可以透過兩個相機之間的基礎矩陣來精細特徵點的影像座標，
也許這樣能讓三角測量還原的3D點座標更為精準。
而你也可以劃出核線來看匹配的情況是否在核線上面。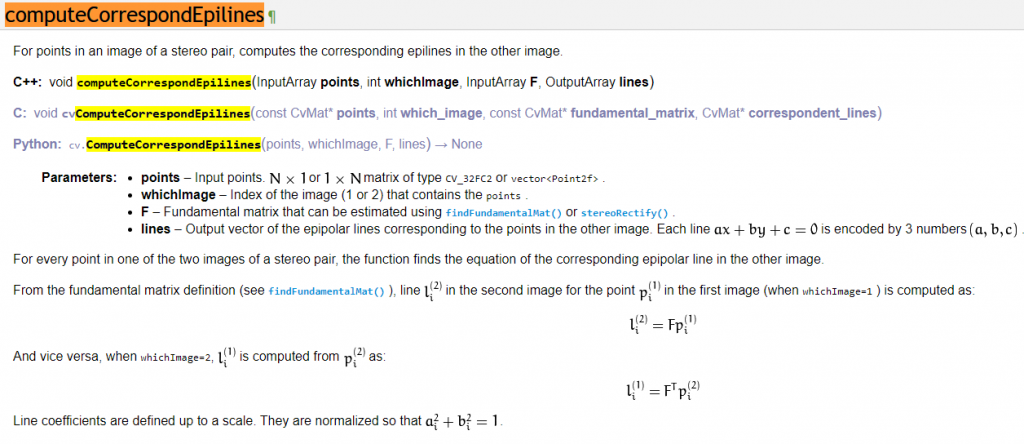

for( i = 0; i < nimages; i++ )
{
    int npt = (int)imagePoints[0][i].size();
    cv::Mat imgpt[2];
    for( k = 0; k < 2; k++ )
    {
        imgpt[k] = cv::Mat(imagePoints[k][i]);
        undistortPoints(imgpt[k], imgpt[k], cameraMatrix[k], distCoeffs[k], cv::Mat(), cameraMatrix[k]);
        computeCorrespondEpilines(imgpt[k], k+1, F, lines[k]);
    }
    for( j = 0; j < npt; j++ )
    {
        double errij = fabs(imagePoints[0][i][j].x*lines[1][j][0] +
                            imagePoints[0][i][j].y*lines[1][j][1] + lines[1][j][2]) +
                       fabs(imagePoints[1][i][j].x*lines[0][j][0] +
                            imagePoints[1][i][j].y*lines[0][j][1] + lines[0][j][2]);
        err += errij;
    }
    npoints += npt;
}
cout << "average reprojection err = " <<  err/npoints << endl;

你可以觀察校正深度相機時如何利用轉換的核線a、b、c來計算再投影誤差，
也可以利用相同的係數來在影像上繪製對應的核線。