前言

這一陣子總統大選幾乎天天有民調，各家調查結果大相逕庭，調查結果相差10~20%，但每一項民調都宣稱『信心水準95%，抽樣誤差為正負3.0%』，照理講不是應該只有 5% (1-95%) 的機率會猜錯嗎? 為什麼每次大選都跌破一大堆眼鏡呢? 基於好奇心，用力研究一下民意調查相關程序及其背後的統計理論基礎，將心得分享一下，期望與大家作進一步的討論，找出問題所在。

民意調查的程序

母體：依中選會推估2020年總統大選全國選舉人數約為1900萬人，投票率7成，有效投票人數約為1400萬人。

調查方法：
以《美麗島電子報》為例，透過『電腦輔助電話訪問系統』(Computer Assisted Telephone Interviewing System，簡稱CATIS)方式進行調查，依選民結構(年齡、性別、偏好政黨等)作『等比例分層隨機抽樣』，以1000人左右的成功完訪作為樣本，進行統計。

調查結果(2019/12/22)：
其他家的民調也大同小異，參見2020年中華民國總統選舉民意調查 - 維基百科，自由的百科全書，擷取其中一張表如下，可以看到有效樣本均為1000人多一點：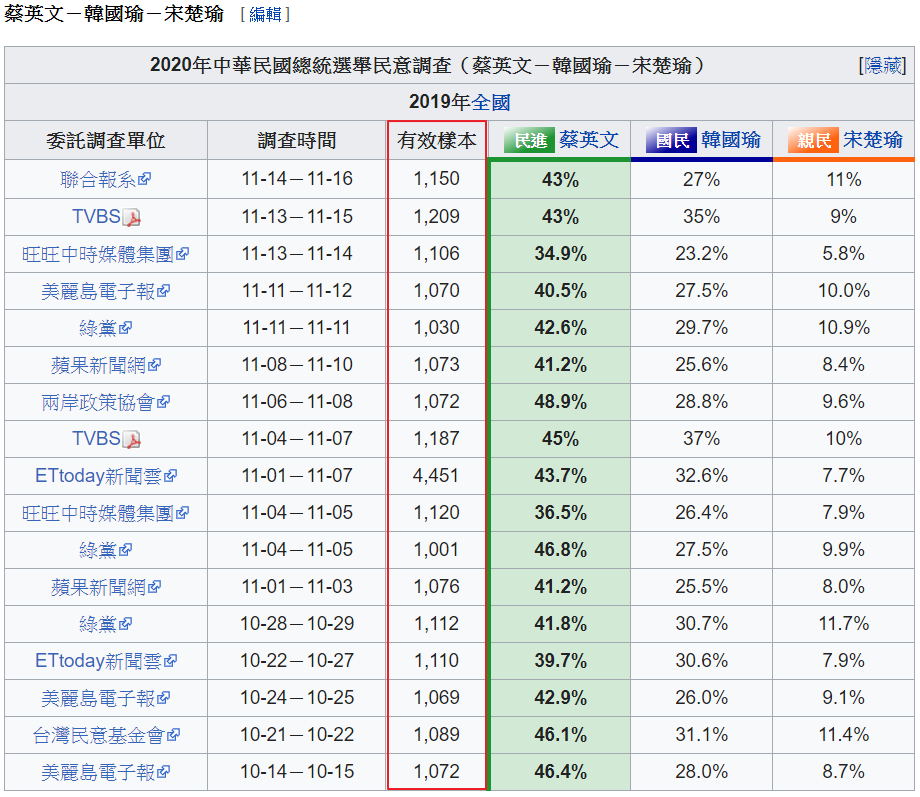

圖. 民意調查彙總表

問題

1. 為什麼調查 1,000人?
2. 如果調查 10,000人 呢?
3. 除了機構效應，還有甚麼因素造成眼鏡掉滿地呢?

定義、定理說明

計算之前，我們先將相關統計量的定義弄清楚，往下讀時先閉目養神一下，或喝口茶提神一下。

一般會假設母體符合『二項分配』(Binomial distribution)，即某人當選的機率為p，因此，

• 平均數(μ) = p
• 標準差(σ) = SQRT(p*(1-p)/n)

其中 SQRT 為開根號。

依照『中央極限定理』(Central Limit Theorem)，隨機抽取大小為n的多批獨立樣本，當批數很大時，其每批樣本的平均數分佈會趨近於常態分配(Normal distribution)，基於此一定理，我們就可以使用常態分配來作區間估計，計算其信賴區間(Confidence interval)，亦即，民意調查設定『信心水準95%』，即信賴區間會落在(μ - 1.96σ, μ + 1.96σ) 之間，換句話說，就是p有95%機率會落在此區間內，參見下圖。

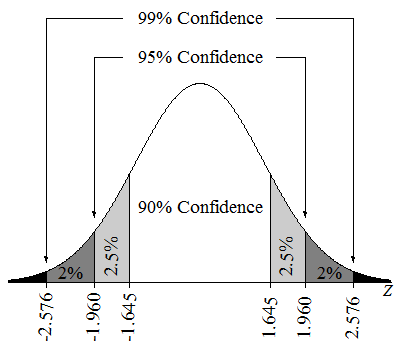
圖. 信心水準(Confidence level)，圖片來源：Hypothesis Testing in Machine Learning: What for and Why

若民調設定抽樣誤差=3%，就是說如果調查結果支持特定候選人的百分比介於(47%,53%)之間，表示在『信心水準95%』的假設下，效果不顯著，無法判別該候選人是否會當選或落選，反之，在(47%,53%)範圍外，我們才可以依據調查結果大膽推論，該候選人會當選或落選。

所需調查人數的計算

所以，基於『信心水準95%，抽樣誤差為正負3.0%』的前提下，我們就可以計算需要調查多少樣本才可滿足此一條件。假設每一個候選人當選與落選的機率是均等的，即p=0.5，抽樣誤差=3%，要抽多少樣本呢? 計算如下：

# 基於
# 1.96 * σ = 0.03 (抽樣誤差)
# σ = (0.5 / sqrt(n))
# ==>
# 1.96 * (0.5 / sqrt(n)) = 0.03
# 將上式移項，求 n
n= (0.5/(0.03/1.96)) ** 2
print(n)

計算得知樣本筆數(n)要大於 1067，故每家民調公司的樣本筆數均為1,000筆左右。

如果調查10,000筆呢?

# n=10,000時，抽樣誤差=?
import math
n=10000
err=1.96 * (0.5 / math.sqrt(n))
print(f'{err*100}%')

計算得知抽樣誤差=0.98%。

同樣在『信心水準95%』的假設下，調查10,000筆，若結果落在(49.02%,50.98%)範圍外，我們就可以大膽推論，該候選人會當選或落選。換個角度說，在同樣的區間估計(47%,53%)下，更多的樣本可以得到更大的信心水準，透過以下計算，幾乎已達6倍標準差了，也就是說調查結果幾乎可以百分之百信任了(真的嗎?)。

# n=10,000時，信心水準=?
import math
n = 10000
s = 0.5 / math.sqrt(n)
 
# 47% 標準化
lower_bound=(0.47 - 0.5)/s
upper_bound=(0.53 - 0.5)/s

# 計算信心水準
i, e = integrate.quad(norms, lower_bound, upper_bound)
print(f'標準差: {s:.2f}')
print(f'標準化: {lower_bound:.2f}, {upper_bound:.2f}')
print(f'信心水準: {i:.2f}')

結果為：
標準差: 0.01
標準化: -6.00, 6.00
信心水準: 1.00

以上就是行之多年的民意調查的理論基礎，看似非常嚴謹，但是歷年的實證結果卻非常差，原因可能如下：

1. 機構效應：調查機構立場不中立，調查問題有引導性。
2. 採市話抽樣：目前手機盛行，已有一大部分家庭未安裝市話，這些人就被排除在樣本之外。
3. 採用電話簿抽樣：電話簿中不登記者約有50%，即母體有一半被排除在樣本之外。
4. 理論遭受質疑：以上理論是以二項分配為基礎，但是大多數的調查是以候選人的支持率為統計基礎，如果是三個候選人，就不是二項分配，而是多項式分配，詳見『民意調查與兩種文化』、『民意調查與兩種文化』。

如果排除以上因素，單就學理探討，以上決定抽樣人數(1,067人)的方法也有缺陷：

1. 與母體人數無關：目前是以1000人去推斷1900萬人，如果台灣人口膨脹至19億人，推測的準確度也是一樣嗎? 依上述得推導，母體大小好像都沒被用到，這問題應該如何解決，我目前也不知道。
2. 上述信賴區間只考慮型一誤差（Type I error），即當H0為真(無法判定當選或落選)時，誤認H1為真(當選或落選)，型一誤差機率為5%。可參閱

如果要額外考慮型二誤差（Type II error），可使用檢定力分析(Power Analysis)，接下來，我們就來看看這種方法計算出來的結果。有關型一誤差、型二誤差，可參閱『淺談機器學習的效能衡量指標』系列文的介紹。

檢定力分析(Power Analysis)

型二誤差(β)：即虛無假設為假時，卻拒絕虛無假設，即兩組候選人有明顯差距，卻誤認無差距。

檢定力(Power)：即型二誤差的檢定能力，如果檢定力不足，就不能排除隨機誤差是造成有差異的原因。一般檢定力會設成0.8以上。

效應值(effect size)：實驗組和控制組之間差異的大小，其絕對值越大表示效應越強，也就是現象越明顯。應用在民調上，就是兩組候選人的差距在多少百分比以上，才被認為有明顯的差異。通常會參考 Cohen's d 效應值統計表來作設定。

Wikipedia 定義的效應值統計表：

分別設定檢定力、效應值後，就可以使用『檢定力分析』計算抽樣人數。筆者直接使用 Python statsmodels 套件可就可以輕易算出來了。

1. 同樣在『信心水準95%』的假設下，檢定力=0.8，效應值=0.1(只要贏10%就算贏)

# 檢定力分析(Power Analysis)
from statsmodels.stats.power import tt_ind_solve_power
tt_ind_solve_power(effect_size=0.1, nobs1 = None, alpha=0.05, power=0.8, ratio=1, alternative='two-sided')

得到結果，應抽樣人數=1570.

2. 設定檢定力=0.9，效應值=0.1

# 檢定力分析(Power Analysis)
from statsmodels.stats.power import tt_ind_solve_power
tt_ind_solve_power(effect_size=0.1, nobs1 = None, alpha=0.05, power=0.9, ratio=1, alternative='two-sided')

得到結果，應抽樣人數=2102.

3. 設定檢定力=0.9，效應值=0.3

# 檢定力分析(Power Analysis)
from statsmodels.stats.power import tt_ind_solve_power
tt_ind_solve_power(effect_size=0.1, nobs1 = None, alpha=0.05, power=0.9, ratio=1, alternative='two-sided')

得到結果，應抽樣人數=175.

顯然，這個方法比現行的民調方法有彈性，也比較週全。

結論

目前民調的理論基礎並不堅實(Solid)，調查結果也因差異很大，又不準確，倍受質疑，到底改善的方向為何，期待統計大神們出來說清楚、講明白，因為台灣一天到晚在選舉，每逢總統大選，幾乎天天有民調，到底要信哪一家民調? 還是只能信上帝?