我在Matters上歸納了這週的技巧總結,如果有興趣可以一起研究。
我的Matters: 前端野人
說明:找出與陣列長度相符合的陣列元素內相成的最大數組
Example:
Input: [1,2,3,4]
Output: [24,12,8,6]
思維:
就以Solution的觀察可以發現,如果走訪陣列的話,索引值指向的元素以外的元素相成可得到當下索引值的最大數,所以依照題型,可以嘗試將每個元素以外的所有元素相成,所以這題目最大的問題是,怎麼找出當下索引值以外的陣列。
Solution 則是利用一左一右的陣列來處理這問題,首先要建立兩個陣列,L跟R
兩個的第一個元素皆為1。而從第二個元素開始的值都是nums[i] * L[i-1]得來,
這樣就可以得出nums從左邊相成的前一個數,另外的R也是相同只是方向相反。
| nums | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| L | 1 | 1 | 2 | 6 |
| numsR | 4 | 3 | 2 | 1 |
|---|---|---|---|---|
| R | 1 | 4 | 12 | 24 |
R需要再反轉一次R.revserse,真正的R為:
| nums | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| R | 24 | 12 | 4 | 1 |
而答案則是answer[i] = L[i] * R[i]得出,原因在於,上面的每個元素值就是各兩邊從當下元素前面所有元素累加的值。
舉例:L[lastIndex]的值就是除了nums[lastIndex]的所有值相成。R[firstIndex]的值就是除了nums[firstIndex]以外相成的值。
而相成之後就剛好是nums[i]以外所有值的總和。
Ans:
var productExceptSelf = function(nums) {
let L = [1]
let R = [1]
let startNum = 1
for(let i = 0 ; i < nums.length-1; i++){
L[i+1] = (L[i+1-1] * nums[i])
}
let numsR = nums.reverse()
for(let i = 0 ; i < nums.length-1 ; i++){
R[i+1] = R[i+1-1] * numsR[i]
}
R = R.reverse()
const answer = []
for(let i = 0 ; i < nums.length; i++){
answer.push(L[i] * R[i])
}
return answer
};
說明:判斷字符是否正確
Example 1:
Input: "()"
Output: True
Example 2:
Input: "(*)"
Output: True
Example 3:
Input: "(*))"
Output: True
思維:
需要左右括號包起來字串才合法。
而*可以代表任一括號,也可以是空字串。
依照Solution的最佳解,則是從 lo == 0來判斷是否合法。
用lo、hi代表左右括號的數量
lo += (則 +1否則-1
hi += )則 +1否則-1
如果hi < 0表示 *或( 可能超過)所以就先跳出,剩下交給lo判斷。
所以如果lo > 0就表示(超過)那就是false,但lo必須讓他至少為0,
原因在於(**是合法的,所以當lo < 0的時候應該要為0,
而如果是(**)(,會因為lo是0又+1 這時又能判斷為false。
下面圖表需想像lo 為負數時 lo = 0 而hi < 0 時則不繼續判斷hi
| lo | hi | answer | |
|---|---|---|---|
| ( | 1 | -1 | false |
| ()) | 1 | -2 | false |
| (** | -1 | -2 | true |
| (**) | -2 | -2 | true |
這題難的點在於,要去假設lo為0來去判斷是否合法,而hi < 0則不運算hi,這是很難從題意去聯想出來的解法。
Ans:
var checkValidString = function(s) {
let lo = 0
let hi = 0
for(let i = 0; i < s.length ; i ++){
lo += s[i] == "(" ? 1 : -1
hi += s[i] != ")" ? 1 : -1
if(hi < 0) break
lo = Math.max(lo,0)
}
return lo == 0
};
說明:從陣列中的0、1判斷有幾個區塊。
Example 1:
Input:
11110
11010
11000
00000
Output: 1
Example 2:
Input:
11000
11000
00100
00011
Output: 3
解析:
這題為DFS的應用,依照演算法走訪,以圖形表達為下圖所呈現:

DFS適合用來探尋未知的節點,DFS會反覆的搜尋任何可達到的節點直到所有節點被發現為止。
因為會反覆的搜尋所以必須要注意,該節點是否已經被走訪過。
而recusion遞迴適合做DFS的基底
如果是照Find the number of islands | Set 1 (Using DFS) - GeeksforGeeks的思維其實我覺得比較不好,他先用hashmap紀錄走訪過的點,並用八個方向來走訪,這樣做不會破壞「島」的大小,但觀念是一樣的。
leetcode普遍解法是在二維陣列的索引範圍內遇到1先算+1並開始從這個array[i][j]的節點開始走訪在陣列的範圍內不斷尋找上下左右是1的節點,找到後改成0。
所以就變成第一個遇到的1就代表一座島的意思,然後再把相鄰的1改成0直到所有方向遇到0為止。
下面則是DFS走訪的程式碼。
const dfs = (i,j,grid) =>{
if(i < 0 || j < 0 || i >= grid.length || j >= grid[i].length || grid[i][j] == 0){
return 0
}
grid[i][j] = 0
dfs(i+1,j,grid)
dfs(i-1,j,grid)
dfs(i,j-1,grid)
dfs(i,j+1,grid)
return 1
}
Ans:
var numIslands = function(grid) {
const dfs = (i,j,grid) =>{
if(i < 0 || j < 0 || i >= grid.length || j >= grid[i].length || grid[i][j] == 0){
return 0
}
grid[i][j] = 0
dfs(i+1,j,grid)
dfs(i-1,j,grid)
dfs(i,j-1,grid)
dfs(i,j+1,grid)
return 1
}
let answer = 0
for(let i = 0 ; i < grid.length ; i++){
for(let j = 0 ; j < grid[i].length ; j++){
if(grid[i][j] == 1) answer += dfs(i,j,grid)
}
}
return answer
};
說明:從起點到終點的最小路徑和。
Example:
Input:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.
思維:
這題可能會聯想到Dijkstra's algorithm,但實際上並沒有這麼複雜,dijkstra是用來記錄起點到每個點的最小路徑,但這題只要算起點到終點的最小路徑和。
這題,以大部分的解法都是使用DP,而運算會分三個部分
1.第一列的每個元素要加前一個元素和。
2.第一行的每個元素要加前一個元素和。
3.中間的梯形路徑要加前一格元素和。
這樣運算後就可以判斷哪個元素更小,以利於加總。
如
第一列grid[i][0] += grid[i-1][0]會變成:
[
[1,3,1],
[2,5,1],
[6,2,1]
]
再運算第一行grid[0][j] += grid[0][j-1]會變成:
[
[1,4,5],
[2,5,1],
[6,2,1]
]
最後計算最小路徑和grid[i][j] += Math.min(grid[i-1][j],grid[i][j-1]),從grid[1][1]開始,而grid[0][1]代表著grid[0][0]+ grid[0][1]的路徑和,grid[1][0]一樣,所以累加起來的最小值就是最小路徑和。走訪次去為:
[
[1, 4 , 5 ],
[2,(2+5),(1+5)],
[6,(2+6),(1+6)]
]
min : 7
Ans:
var minPathSum = function(grid) {
const row = grid.length
const col = grid[0].length
// 第一列
for(let i = 1 ; i < row ; i++){
grid[i][0] += grid[i-1][0]
}
// 第一行
for(let j = 1 ; j < col ; j++){
grid[0][j] += grid[0][j-1]
}
// 中間梯形路徑
for(let i = 1 ; i < row ; i++){
for(let j = 1 ; j < col ; j++){
grid[i][j] += Math.min(grid[i-1][j],grid[i][j-1])
}
}
return grid[row-1][col-1]
};
說明:找出反轉矩陣中的值。
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1
思維:
這題看似很難,但卻只用幾個直覺的判斷是就能完成。搜尋中要做幾個判斷。
1.找出target的索引值,沒有就回傳-1
2.但如果target是陣列中的元素就要回傳索引值。如arr = [1,4],target =4 ,ans =1
Ans:
var search = function(nums, target) {
if(nums.some(num => num == target)){
if(target === nums.find(num => num === target) ){
return nums.findIndex(num => num === target)
}else{
return nums[target]
}
}else{
return -1
}
};
說明:二元樹的Preorder Traversal。
Example 1:
Input: [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]
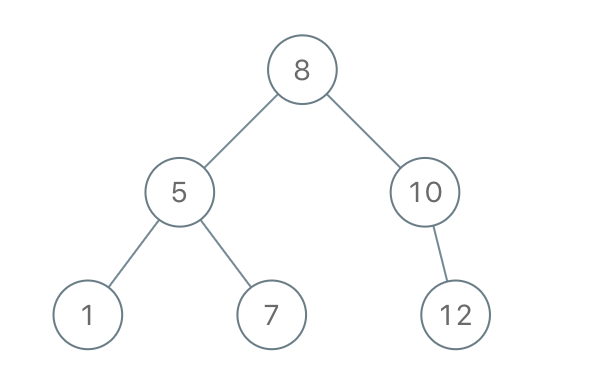
思維:
就是建立二元搜尋數的Preorder Traversal,這個直接研究資料結構最好。
我覺得有一個leetcoder的思維最精闢,因為二元搜尋數通常是用list處理,所以最好的方式就是用recusion,而這題是用preorder.slice(1).filter去分類left跟right。
陣列大概會變成:
[8,5,1,7,10,12], //建立root = 8;
[5,1,7], root = 8 ,left tree
[10,12], root = 8 ,right tree
[1], root = 5 ,left tree
[7] root = 5 ,right tree
[] roor = 10,left tree
[12], root = 10,right tree
Ans:
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
var bstFromPreorder = function(preorder) {
if(preorder.length === 0) return null
if(preorder.length === 1) return new TreeNode(preorder[0])
let root = new TreeNode(preorder[0])
let left = bstFromPreorder(preorder.slice(1).filter(ele => ele < preorder[0]))
let right = bstFromPreorder(preorder.slice(1).filter(ele => ele > preorder[0]))
if(root) root.left = left
if(root) root.right = right
return root
};
這題我不現在做,原因在於這是新的題目,很像是資料結構的算法,依我現在能力可能不能用高明的解法去處理,所以我會過一陣子才會回來解。
