2020.06.24 更新錯誤的Schwefel,現在已經收斂到跟原作者一樣好了
本篇主要是紀錄Adaptive Particle Swarm Optimization的閱讀心得。
最近腦子動到想用PSO來訓練神經網路,所以蒐集了一些相關資料,預計將分享5篇文章
原文的粒子定義如下,在一個D維度解空間中,粒子i的速度和位置定義如下: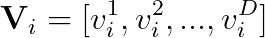
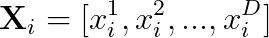
粒子i在任意維度d的速度和位置更新公式: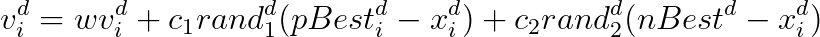
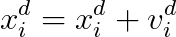
原文提到PSO有兩個版本,分別是global-version PSO(GPSO)和local-version PSO(LPSO)。在Advances of Computational Intelligence in Industrial Systems的第9頁和Manufacturing Optimization through Intelligent Techniques的第41頁有提到GPSO和LPSO的差別以及優缺點:
相較於傳統PSO,APSO在計算過程中多了演化狀態評估(Evolutionary State Estimation, ESE)和菁英學習策略(Elitist Learning Strategy, ELS)兩個步驟。
不囉嗦,直接貼圖。如果刪去流程圖的第三步驟,那就是傳統PSO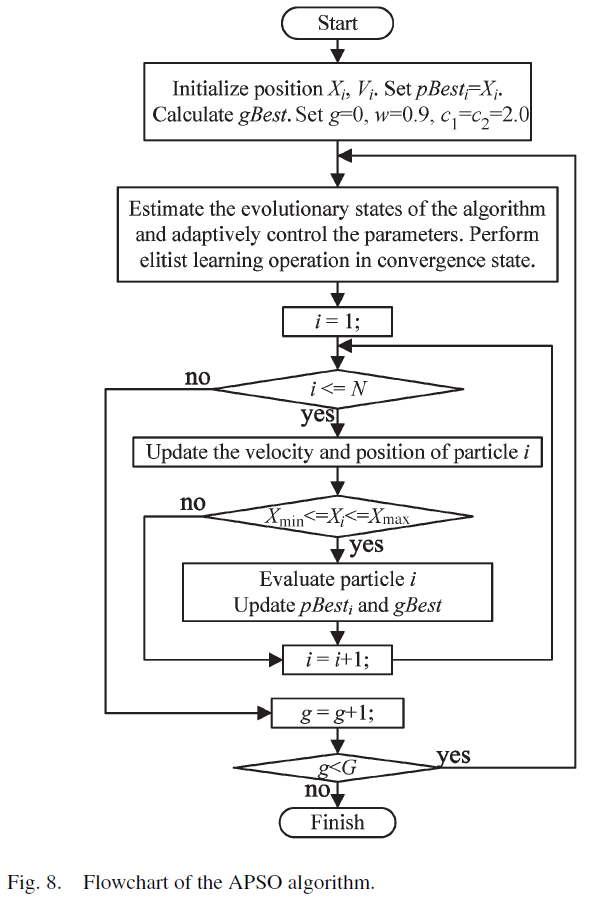
作者定義的加速度限制為解空間的20%,也就是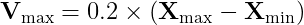
由於作者沒有特別說明,因此初始加速度我令為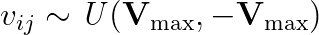
根據每次迭代粒子的分布情形來調整w、c1、c2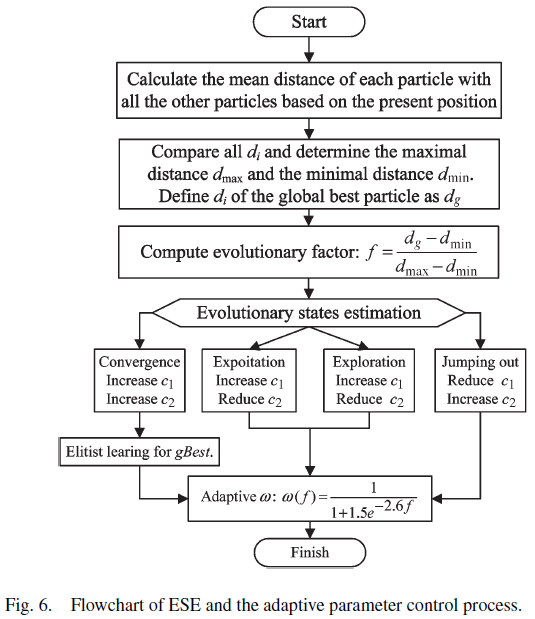
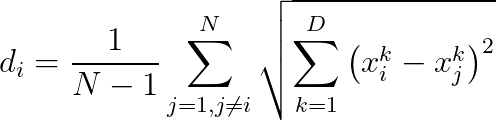
很明顯這是在求L2範數(歐式距離),然後為了編程方便,我把式子簡化如下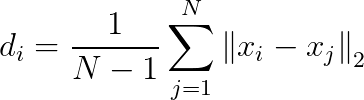
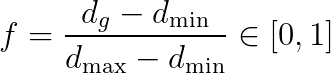
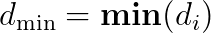
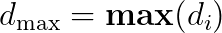


原文沒有完整說明規則庫內容,我只能透過內文的範例進行推論,結果如下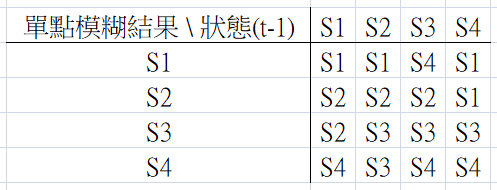
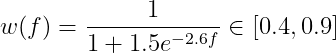
原文的初始慣性權重為0.9
加速度常數的範圍需落在,初始值為2.0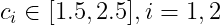
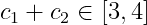
如果c1+c2大於指定範圍,則用下式調整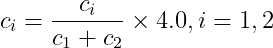
根據不同的狀態,以加速度率(acceleration rate)調整加速度常數
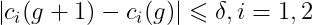
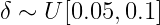
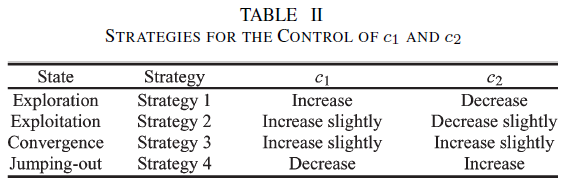
原文有明確定義所謂的輕微是指0.5倍的加速度率,因此可以得到下面結論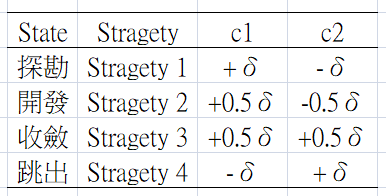
想像一下,某個粒子要更新自己的加速度,但是他發現自己就是pBest,同時他又是gBest,所以加速度更新公式的三個子項中就有2項是0。由於這個粒子在該次代沒有任何可以學習的對象,因此他本次移動是毫無根據的,這會間接導致粒子子求解速度被拖慢,因此制定一個擾動策略(類似基因算法的突變)來嘗試得到更好的gBest。當然,不是每次擾動都會得到更好的gBest,但我們可以取代最差的粒子,使得整體表現變得更均勻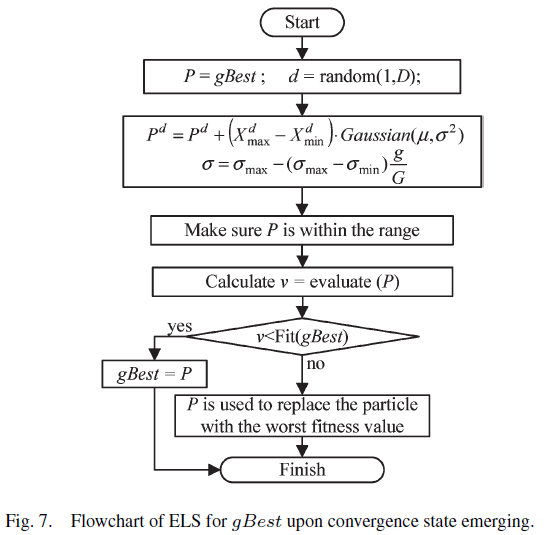
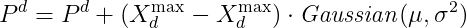
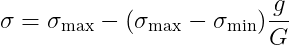
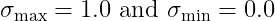
我自己對5-2作了修改,如下
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
class APSO():
def __init__(self, fit_func, num_dim, num_particle=20, max_iter=500,
x_max=1, x_min=-1, w_max=0.9, w_min=0.4, c1=2.0, c2=2.0, k=0.2):
self.fit_func = fit_func
self.num_dim = num_dim
self.num_particle = num_particle
self.max_iter = max_iter
self.x_max = x_max
self.x_min = x_min
self.w = w_max
self.w_max = w_max
self.w_min = w_min
self.c1 = c1
self.c2 = c2
self.k = k
self._iter = 1
self.bestX_idx = -1
self.worstX_idx = -1
# case1. 僅初始化
self.delta = np.random.uniform(high=0.1, low=0.05, size=1)
self.state = 1
self.rulebase = [[1, 1, 4, 1],
[2, 2, 2, 1],
[2, 3, 3, 3],
[4, 3, 4, 4]]
self.gBest_curve = np.zeros(self.max_iter)
self.X = np.random.uniform(size=[self.num_particle, self.num_dim])*(self.x_max-self.x_min) + self.x_min
self.V = np.random.uniform(size=[self.num_particle, self.num_dim])*(self.x_max-self.x_min) + self.x_min
self.v_max = self.k*(self.x_max-self.x_min)
self.pBest_X = self.X.copy()
self.pBest_score = self.fit_func(self.X).copy()
self.X_score = self.pBest_score.copy()
self.gBest_X = self.pBest_X[self.pBest_score.argmin()].copy()
self.gBest_score = self.pBest_score.min().copy()
self.gBest_curve[0] = self.gBest_score.copy()
self.bestX_idx = self.pBest_score.argmin()
self.worstX_idx = self.pBest_score.argmax()
def ESE(self):
# step 1.
d_set = np.zeros(self.num_particle)
for i in range(self.num_particle):
d_set[i] = np.sum(np.linalg.norm((self.X[i, :].reshape(1, self.num_dim)-self.X), ord=2, axis=1))\
/(self.num_particle-1)
# step 2.
dmax = np.max(d_set)
dmin = np.min(d_set)
dg = d_set[self.bestX_idx].copy()
# 我自己額外加的,防止崩潰
if dmax==dmin==dg==0:
f = 0
else:
f = (dg-dmin)/(dmax-dmin)
if not(0<=f<=1):
print('f='+str(np.round(f, 3))+' 超出範圍[0, 1]!!!')
if f>1:
f = 1
elif f<0:
f = 0
# step 3.
singleton = np.zeros(4)
if 0<=f<=0.4:
singleton[0] = 0
elif 0.4<f<=0.6:
singleton[0] = 5*f - 2
elif 0.6<f<=0.7:
singleton[0] = 1
elif 0.7<f<=0.8:
singleton[0] = -10*f + 8
elif 0.8<f<=1:
singleton[0] = 0
if 0<=f<=0.2:
singleton[1] = 0
elif 0.2<f<=0.3:
singleton[1] = 10*f - 2
elif 0.3<f<=0.4:
singleton[1] = 1
elif 0.4<f<=0.6:
singleton[1] = -5*f + 3
elif 0.6<f<=1:
singleton[1] = 0
if 0<=f<=0.1:
singleton[2] = 1
elif 0.1<f<=0.3:
singleton[2] = -5*f + 1.5
elif 0.3<f<=1:
singleton[2] = 0
if 0<=f<=0.7:
singleton[3] = 0
elif 0.7<f<=0.9:
singleton[3] = 5*f - 3.5
elif 0.9<f<=1:
singleton[3] = 1
if np.max(singleton)==np.min(singleton)==0:
print('因為f超出範圍[0, 1],所以模糊推論異常!!!')
t = np.argmax(singleton)
t_1 = self.state - 1
self.state = self.rulebase[int(t)][int(t_1)]
# (10)
self.w = 1/(1+1.5*np.exp(-2.6*f))
if not(self.w_min<=self.w<=self.w_max):
print('w='+str(np.round(self.w, 3))+' 超出範圍[0.4, 0.9]!!!')
if self.w<self.w_min:
self.w = self.w_min
elif self.w>self.w_max:
self.w = self.w_max
# (11)
if self.state==1:
self.c1 = self.c1 + self.delta
self.c2 = self.c2 - self.delta
if self.state==2:
self.c1 = self.c1 + 0.5*self.delta
self.c2 = self.c2 - 0.5*self.delta
if self.state==3:
self.c1 = self.c1 + 0.5*self.delta
self.c2 = self.c2 + 0.5*self.delta
self.ELS()
if self.state==4:
self.c1 = self.c1 - self.delta
self.c2 = self.c2 + self.delta
if not(1.5<=self.c1<=2.5):
# print('c1='+str(np.round(self.c1, 3))+' 超出範圍[1.5, 2.5]!!!')
if self.c1<1.5:
self.c1 = 1.5
elif self.c1>2.5:
self.c1 = 2.5
if not(1.5<=self.c2<=2.5):
# print('c2='+str(np.round(self.c2, 3))+' 超出範圍[1.5, 2.5]!!!')
if self.c2<1.5:
self.c2 = 1.5
elif self.c2>2.5:
self.c2 = 2.5
# (12)
if not(3<=self.c1+self.c2<=4):
# print('c1='+str(np.round(self.c1, 3))+' + c2='+str(np.round(self.c2, 3))+' 超出範圍[3, 4]!!!')
self.c1, self.c2 = 4.0*self.c1/(self.c1+self.c2), 4.0*self.c2/(self.c1+self.c2)
def ELS(self):
rho = 1 - ((1-0.1)*self._iter/self.max_iter)
d = np.random.randint(low=0, high=self.num_dim, size=1)
P = self.gBest_X.copy()
P[d] = P[d] + (self.x_max[d]-self.x_min[d])*np.random.normal(loc=0.0, scale=rho**2, size=1)
if P[d]>self.x_max[d]: P[d] = self.x_max[d]
if P[d]<self.x_min[d]: P[d] = self.x_min[d]
score = self.fit_func(P.reshape(1, -1))
if score<self.gBest_score:
self.gBest_X = P.copy()
self.gBest_score = score.copy()
else:
# # case1. 原文版本
# self.X[self.worstX_idx, :] = P.copy()
# case2. 我的版本
if score<self.X_score[self.worstX_idx]:
self.X[self.worstX_idx, :] = P.copy()
if score<np.max(self.pBest_score):
idx = np.argmax(self.pBest_score)
self.pBest_score[idx] = score.copy()
self.pBest_X[idx, :] = P.copy()
def opt(self):
while(self._iter<self.max_iter):
# case2. 每代更新
# self.delta = np.random.uniform(high=0.1, low=0.05, size=1)
self.bestX_idx = self.X_score.argmin()
self.worstX_idx = self.X_score.argmax()
self.ESE()
R1 = np.random.uniform(size=(self.num_particle, self.num_dim))
R2 = np.random.uniform(size=(self.num_particle, self.num_dim))
for i in range(self.num_particle):
self.V[i, :] = self.w * self.V[i, :] \
+ self.c1 * (self.pBest_X[i, :] - self.X[i, :]) * R1[i, :] \
+ self.c2 * (self.gBest_X - self.X[i, :]) * R2[i, :]
self.V[i, self.v_max < self.V[i, :]] = self.v_max[self.v_max < self.V[i, :]]
self.V[i, -self.v_max > self.V[i, :]] = -self.v_max[-self.v_max > self.V[i, :]]
self.X[i, :] = self.X[i, :] + self.V[i, :]
self.X[i, self.x_max < self.X[i, :]] = self.x_max[self.x_max < self.X[i, :]]
self.X[i, self.x_min > self.X[i, :]] = self.x_min[self.x_min > self.X[i, :]]
score = self.fit_func(self.X[i, :])
self.X_score[i] = score.copy()
if score<self.pBest_score[i]:
self.pBest_X[i, :] = self.X[i, :].copy()
self.pBest_score[i] = score.copy()
if score<self.gBest_score:
self.gBest_X = self.X[i, :].copy()
self.gBest_score = score.copy()
self.gBest_curve[i] = self.gBest_score.copy()
self._iter = self._iter + 1
def plot_curve(self):
plt.figure()
plt.title('loss curve ['+str(round(self.gBest_curve[-1], 3))+']')
plt.plot(self.gBest_curve, label='loss')
plt.grid()
plt.legend()
plt.show()
from APSO import APSO
import numpy as np
import time
import pandas as pd
np.random.seed(42)
def Sphere(x):
if x.ndim==1:
x = x.reshape(1, -1)
return np.sum(x**2, axis=1)
def Schwefel_P222(x):
if x.ndim==1:
x = x.reshape(1, -1)
return np.sum(np.abs(x), axis=1) + np.prod(np.abs(x), axis=1)
def Quadric(x):
if x.ndim==1:
x = x.reshape(1, -1)
outer = 0
for i in range(x.shape[1]):
inner = np.sum(x[:, :i+1], axis=1)**2
outer = outer + inner
return outer
def Rosenbrock(x):
if x.ndim==1:
x = x.reshape(1, -1)
left = x[:, :-1].copy()
right = x[:, 1:].copy()
return np.sum(100*(right - left**2)**2 + (left-1)**2, axis=1)
def Step(x):
if x.ndim==1:
x = x.reshape(1, -1)
return np.sum(np.round((x+0.5), 0)**2, axis=1)
def Quadric_Noise(x):
if x.ndim==1:
x = x.reshape(1, -1)
matrix = np.arange(x.shape[1])+1
return np.sum((x**4)*matrix, axis=1)+np.random.rand(x.shape[0])
def Schwefel(x):
if x.ndim==1:
x = x.reshape(1, -1)
return -1*np.sum(x*np.sin(np.abs(x)**.5), axis=1)
def Rastrigin(x):
if x.ndim==1:
x = x.reshape(1, -1)
return np.sum(x**2 - 10*np.cos(2*np.pi*x) + 10, axis=1)
def Noncontinuous_Rastrigin(x):
if x.ndim==1:
x = x.reshape(1, -1)
outlier = np.abs(x)>=0.5
x[outlier] = np.round(2*x[outlier])/2
return np.sum(x**2 - 10*np.cos(2*np.pi*x) + 10, axis=1)
def Ackley(x):
if x.ndim==1:
x = x.reshape(1, -1)
left = 20*np.exp(-0.2*(np.sum(x**2, axis=1)/x.shape[1])**.5)
right = np.exp(np.sum(np.cos(2*np.pi*x), axis=1)/x.shape[1])
return -left - right + 20 + np.e
def Griewank(x):
if x.ndim==1:
x = x.reshape(1, -1)
left = np.sum(x**2, axis=1)/4000
right = np.prod( np.cos(x/((np.arange(x.shape[1])+1)**.5)), axis=1)
return left - right + 1
d = 30
g = 1000
p = 20
times = 30
table = np.zeros((2, 11))
for i in range(times):
x_max = 100*np.ones(d)
x_min = -100*np.ones(d)
optimizer = APSO(fit_func=Sphere, num_dim=d, num_particle=p, max_iter=g, x_max=x_max, x_min=x_min)
start = time.time()
optimizer.opt()
end = time.time()
table[0, 0] += optimizer.gBest_score
table[1, 0] += end - start
x_max = 10*np.ones(d)
x_min = -10*np.ones(d)
optimizer = APSO(fit_func=Schwefel_P222, num_dim=d, num_particle=p, max_iter=g, x_max=x_max, x_min=x_min)
start = time.time()
optimizer.opt()
end = time.time()
table[0, 1] += optimizer.gBest_score
table[1, 1] += end - start
x_max = 100*np.ones(d)
x_min = -100*np.ones(d)
optimizer = APSO(fit_func=Quadric, num_dim=d, num_particle=p, max_iter=g, x_max=x_max, x_min=x_min)
start = time.time()
optimizer.opt()
end = time.time()
table[0, 2] += optimizer.gBest_score
table[1, 2] += end - start
x_max = 10*np.ones(d)
x_min = -10*np.ones(d)
optimizer = APSO(fit_func=Rosenbrock, num_dim=d, num_particle=p, max_iter=g, x_max=x_max, x_min=x_min)
start = time.time()
optimizer.opt()
end = time.time()
table[0, 3] += optimizer.gBest_score
table[1, 3] += end - start
x_max = 100*np.ones(d)
x_min = -100*np.ones(d)
optimizer = APSO(fit_func=Step, num_dim=d, num_particle=p, max_iter=g, x_max=x_max, x_min=x_min)
start = time.time()
optimizer.opt()
end = time.time()
table[0, 4] += optimizer.gBest_score
table[1, 4] += end - start
x_max = 1.28*np.ones(d)
x_min = -1.28*np.ones(d)
optimizer = APSO(fit_func=Quadric_Noise, num_dim=d, num_particle=p, max_iter=g, x_max=x_max, x_min=x_min)
start = time.time()
optimizer.opt()
end = time.time()
table[0, 5] += optimizer.gBest_score
table[1, 5] += end - start
x_max = 500*np.ones(d)
x_min = -500*np.ones(d)
optimizer = APSO(fit_func=Schwefel, num_dim=d, num_particle=p, max_iter=g, x_max=x_max, x_min=x_min)
start = time.time()
optimizer.opt()
end = time.time()
table[0, 6] += optimizer.gBest_score
table[1, 6] += end - start
x_max = 5.12*np.ones(d)
x_min = -5.12*np.ones(d)
optimizer = APSO(fit_func=Rastrigin, num_dim=d, num_particle=p, max_iter=g, x_max=x_max, x_min=x_min)
start = time.time()
optimizer.opt()
end = time.time()
table[0, 7] += optimizer.gBest_score
table[1, 7] += end - start
x_max = 5.12*np.ones(d)
x_min = -5.12*np.ones(d)
optimizer = APSO(fit_func=Noncontinuous_Rastrigin, num_dim=d, num_particle=p, max_iter=g, x_max=x_max, x_min=x_min)
start = time.time()
optimizer.opt()
end = time.time()
table[0, 8] += optimizer.gBest_score
table[1, 8] += end - start
x_max = 32*np.ones(d)
x_min = -32*np.ones(d)
optimizer = APSO(fit_func=Ackley, num_dim=d, num_particle=p, max_iter=g, x_max=x_max, x_min=x_min)
start = time.time()
optimizer.opt()
end = time.time()
table[0, 9] += optimizer.gBest_score
table[1, 9] += end - start
x_max = 600*np.ones(d)
x_min = -600*np.ones(d)
optimizer = APSO(fit_func=Griewank, num_dim=d, num_particle=p, max_iter=g, x_max=x_max, x_min=x_min)
start = time.time()
optimizer.opt()
end = time.time()
table[0, 10] += optimizer.gBest_score
table[1, 10] += end - start
table = table / times
table = pd.DataFrame(table)
table.columns=['Sphere', 'Schwefel_P222', 'Quadric', 'Rosenbrock', 'Step', 'Quadric_Noise', 'Schwefel',
'Rastrigin', 'Noncontinuous_Rastrigin', 'Ackley', 'Griewank']
table.index = ['mean score', 'mean time']
這邊主要是探討原文的ELS和我的ELS間對計算結果的差異,以及delta是要在每代都更新一次或者在初始化階段完成定義後就不再更動,因此會有四個組合的比較。
因為不想等太久,所以
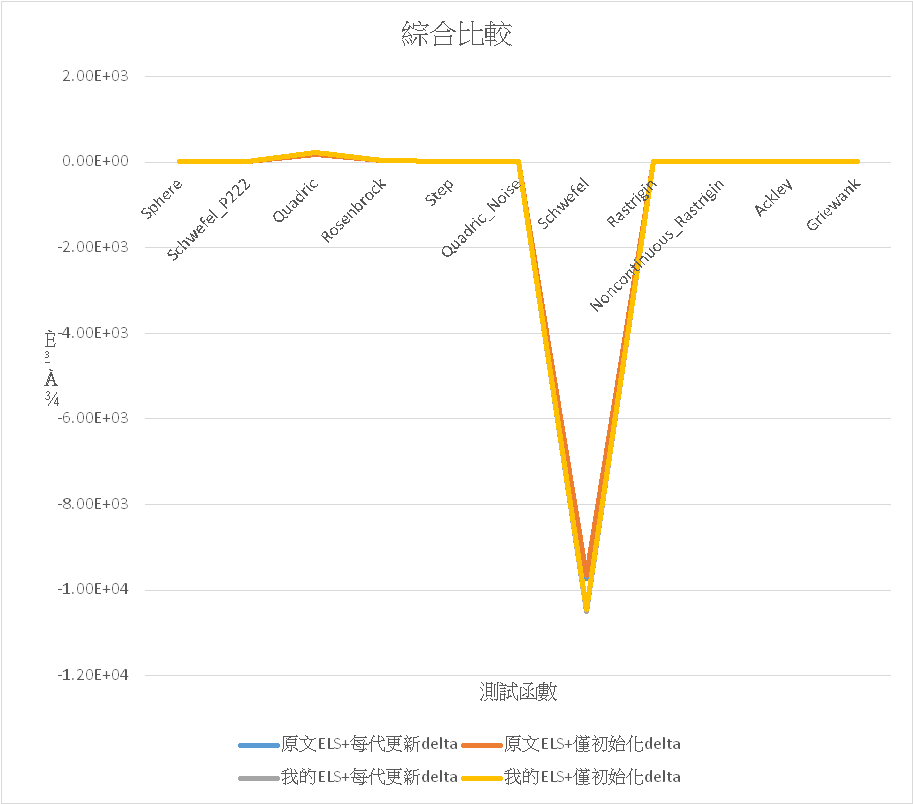
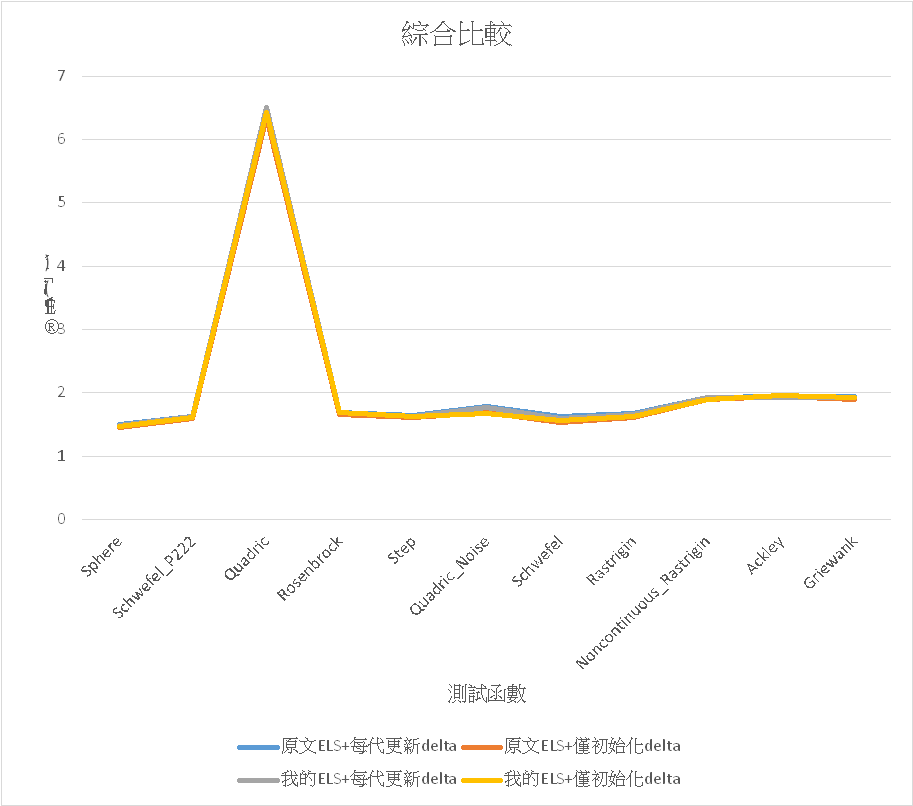
然後是採我的ELS+delta部每代更新的方式,將最大迭代g改成10000後其他條件不變的結果
