前言

今天會以昨天講的TD Learning，來介紹兩種TD Learning中最有名的方法，Sarsa與Q Learning。

Sarsa

昨天TD Learning中的Value Function更新方式為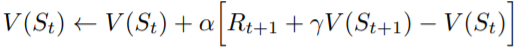

而為了要進行policy improvement，跟Monte Carlo Method一樣，通常會用來取代。

現在公式中的要換成的話，我們的應該要選擇甚麼才對呢？

一種方法是以當前policy的action來決定，我們以這個policy得到的Value值來做更新。更新完後再improvement我們的policy，可以證明最後能夠得到真正的optimal policy。也可以用GPI的圖來看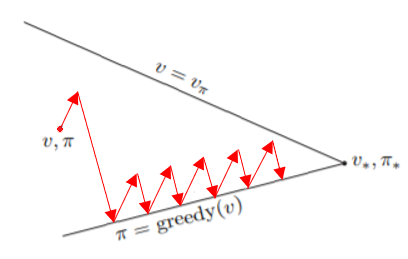

每次都往目前policy選擇的行為來更新，而policy又為當前Value的-greedy policy，所以最後會往optimal policy的方向移動。

根據上述我們用來當作的值，其中為下個時間點中，policy所做的action。

從演算法比較好理解：

Expected sarsa

上述方法收斂的速度沒有很快，原因是因為我的的policy為-greedy policy，如果我們在選擇到隨機action的話，更新後的有可能會偏離真實值。

好的估測的方式是用期望值來計算：，可以保證會以更正確的方向來更新。
所以我們可以將上面的算法改為：

Sarsa與Expected Sarsa的更新類似於stochastic-gradient與gradient的關係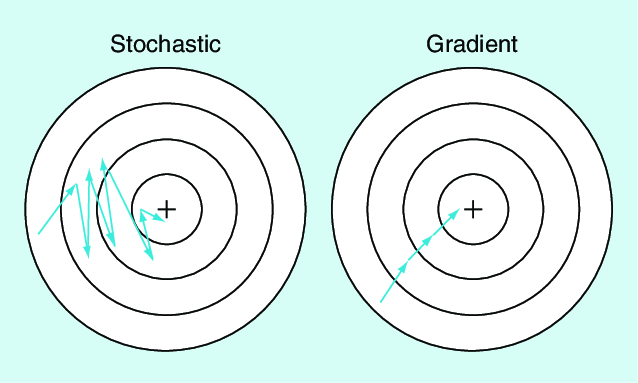

圖片取自https://www.researchgate.net/figure/Stochastic-gradient-descent-compared-with-gradient-descent_fig3_328106221

Sarsa相當於stochastic-gradient
Expected Sarsa相當於gradient

Sarsa的更新不會直接往optimal policy的的更新不會直接往optimal policy的方向走，而是有點凌亂的前進，但最後一樣會收斂至optimal policy。

Q Learning

另一種找Value Function的方法是直接從optimal value function中更新，也就是，每次都以optimal value function更新，可以保證我們快速收斂至optimal value function。

演算法與Sarsa很像，只要改為就好：

總結

學會上面的方法後，基本上大多數有限state的環境都能夠解決。明天將會實際寫code來實現上面的演算法，並稍微介紹一下兩者的優缺點。