前言

dyna-Q是一種運用model與value來一起更新Value Function的方法。在與環境互動有困難的時候相當有用。

Model

model的概念很簡單，就是Agent理解到的環境的知識。經過與環境的互動，Agent會越來越能知道環境中的dynamic，當Agent在狀態上，Agent不需要實際與環境互動，就能估計每個Action會對應到哪個狀態。

可以想像在現實世界中，你透過書上或是新聞上知道從高處掉落會受傷，那下次你在高處時，不需要自己本身從高處烙下，也能知道該行為是不好的。這就稱為你理解的環境中的Model。但Model不一定是完整的，你已經知道從高處落下會受傷，但你並不知道從5公尺高落下會不會受傷，要等到你有其他知識或著例子來告訴你這些知識來提升你的model才行。

Dyna-Q

假如我們的model完整，理論上就能解決所有Reinforcement Learning的問題，只要運用前幾天的policy iteration或value iteration就能找到最佳解。要model完整我們需要一直sample，只要sample數夠多就能達到。但看看前幾天Taxi的例子，光是state就有500個，action又有6個，要每個state與action重複sample好幾次顯然不夠實際。

Dyna-Q就是為了解決這種情況，將q learning與model一起使用，將sample得到的reward值，用來更新Value Function與Model，再用model來更新Value Function。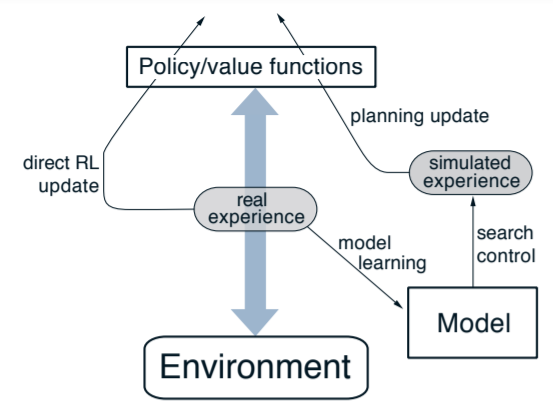

我們稱用model預測下個state這個動作為planning。從圖上可以看到，有一部分的real experience通過direct RL update更新Value，這部分就是熟悉的q learning；另一部分則經過model，再透過model模擬環境的行為更新Value。

代碼也是相當簡單，除了q learning的部分，額外多了n次的planning來更新Value

只要model預測的準確的話(環境的隨機性小，像是迷宮等等)，dyna-Q的收斂速度會比q learning還快許多。

先匯入必要套件

import numpy as np
import sys
from collections import defaultdict
import random
import matplotlib.pyplot as plt

準備我們的環境

class Maze:
    def __init__(self):
        self.pos = (3, 0)
        self.barrier = (0, 7)
        self.action_space = 4

    def reset(self):
        self.barrier = (0, 7)
        self.pos = (3, 0)
        return self.pos, 0, False

    def step(self, action):
        if action == 0: # left
            new_pos = (self.pos[0] - 1, self.pos[1])
        elif action == 1: # up
            new_pos = (self.pos[0], self.pos[1] + 1)
        elif action == 2: # right
            new_pos = (self.pos[0] + 1, self.pos[1])
        elif action == 3: # down
            new_pos = (self.pos[0], self.pos[1] - 1)

        if new_pos[0] < 0 or new_pos[0] > 8 or new_pos[1] < 0 or new_pos[1] > 5 or (new_pos[1] == 2 and self.barrier[0] <= new_pos[0] <= self.barrier[1]):
            new_pos = self.pos
        self.pos = new_pos
        if self.pos[0] == 8 and self.pos[1] == 5:
            return self.pos, 1, True

        return self.pos, 0, False

環境為簡單的gridworld，走到終點reward為1，其餘為0。中間有障礙不能通過。看起來像這樣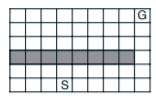

接著實作dyna-Q演算法：

gamma = 0.95
epsilon = 0.1
alpha = 1.0
env = Maze()

def choose_action(state, Q):
    if np.random.rand() < epsilon:
        return np.random.randint(env.action_space)
    else:
        values = Q[state]
        return np.random.choice([action for action, value in enumerate(values) if value == np.max(values)])

def q_update_value(state, action, reward, next_state, done, Q):
    if done:
        Q[state][action] += alpha * (reward - Q[state][action])
    else:
        Q[state][action] += alpha * (reward + gamma * np.max(Q[next_state]) - Q[state][action])
        
def run_q_learning(num_episodes, n = 50, render = False, planning = False):
    Q = defaultdict(lambda: np.zeros(env.action_space))
    rewards = 0
    cumulative_reward = []
    model = {}
    for i in range(num_episodes):
        state, reward, done = env.reset()
        while True:
            action = choose_action(state, Q)
            next_state, reward, done = env.step(action)
            q_update_value(state, action, reward, next_state, done, Q)
            model[(state, action)] = (reward, next_state, done)
            if planning:
                for _ in range(50):
                    (S, A), (R, S_, done_) = random.choice(list(model.items()))
                    q_update_value(S, A, R, S_, done_, Q)
            rewards += reward
            cumulative_reward.append(rewards)
            if done:
                break
            state = next_state
        print(f'\repisode: {i + 1}/{num_episodes}', end = '')
        sys.stdout.flush()
    return cumulative_reward

用dict來記錄走過的model，再用model的經驗更新n次，可參考上面演算法。

注意這邊choose_action我將原本q learning中的np.argmax改成random.choice，這是因為np.argmax在有兩個以上相同最大值時，不會有隨機選擇。

與一般Q Learning做比較，看哪個算法收斂較快

cumulative_reward_planning = run_q_learning(150, True)
cumulative_reward = run_q_learning(150)

plt.plot(cumulative_reward_planning)
plt.plot(cumulative_reward)
plt.legend(['dyna-Q', 'Q Learning'])
plt.ylabel('cumulative reward')
plt.xlabel('time steps')
plt.show()

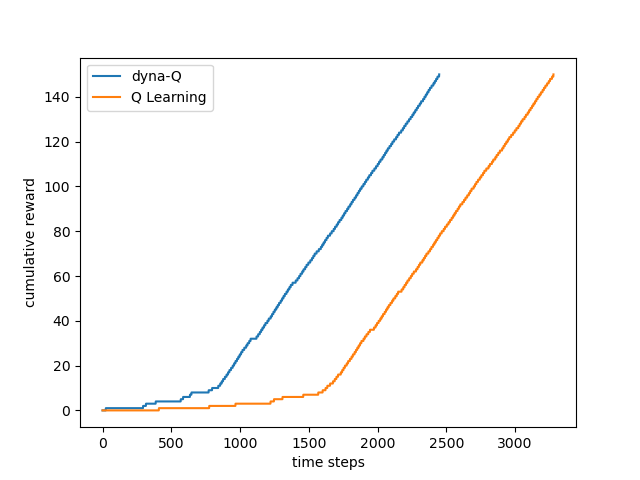
從圖片上可以看到dyna-Q在700 steps後就能找到最佳路徑，而Q Learning要等到約1600steps後才能找到最佳路徑。

總結

如果環境會隨時間改變的話，dyna-Q記錄到的model可能就不準確，可以使用更進階的dyna-Q+來解決，明天將會介紹。dyna-Q也有deep的版本來達成更複雜的任務。運用model來學習在reinforcement learning裡是很重要的，現實生活中我們不一定能都與環境互動，所以model是不可或缺的。