前言

在介紹n-step Learning之前，我們用cliffwalking來比較Q Learning與Sarsa之間的差異，之後再簡單介紹一下n-step Learning的做法。

Cliffwalking

先來介紹gym裡面的cliffwalking環境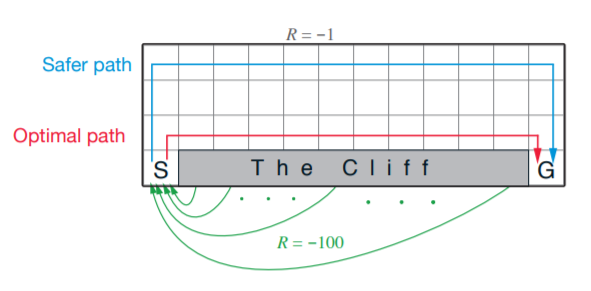

只要經過懸崖(Cliff)，就會回到起始點S，並得到reward -100；其餘step則為-1。
一種較安全的走法就是從上方遠離懸崖的地方走，而最佳路徑則是沿著懸崖邊前進。

匯入需要的參數

import gym
import numpy as np
import sys
from collections import defaultdict

env = gym.make('CliffWalking-v0')

gamma = 1.0
epsilon = 0.1
alpha = 0.5

Agent的程式碼與昨天一樣，這邊就不重複了。

run_sarsa(500, True)
print('------------------------------')
run_q_learning(500, True)

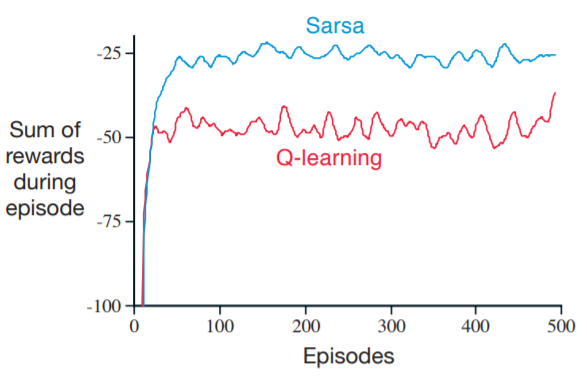
觀察兩種演算法得到的路徑，Q Learning前進的路線為最短路徑，而Sarsa則是偏好較安全的路線。造成這種差異的原因是-greedy，當走在懸崖邊時，有的機率選擇隨機行為，就有機會跌落山谷。

Q Learning在更新過程中是以max來決定更新的方向，所以假設某個action會跌落山谷，Q Learning並不會以該action來更新，所以對Value Function的影響不大；Sarsa則剛好相反，Sarsa會以下一步的行為來更新，如果下一步會跌入山谷，Sarsa將會大幅減少該State的Value，以至於下個episode不會再走到懸崖邊。

從上例可以發現，Sarsa走的路線相較於Q Learning更為保守。在此例中，使用-greedy的Sarsa效能比Q Learning還要好。

很多教學只提及Q Learning，導致許多人認為Q Learning比Sarsa更好用，事實上兩種算法的使用情形要依照環境來做選擇

n-step TD Learning

在Monte Carlo中，Expected return定義為：

在Temporal Difference中，Expected return定義為：

Temporal Difference不一定只依後一個state來更新。事實上，之前學到的TD Learning稱為1-step TD，我們可以在TD與Monte Carlo中做平衡，稱為n-step TD。

更新方式很簡單，只要將擴展TD中的公式：

其中，指的是到的expected return。

算法看似很複雜，其實只是將原本的部分，移到n step後再算，中間則用reward取代。
而如果遇到Final State，則提前結束。

如果要實現n-step Q Learning的話，我們就必須引入importance sampling。可參考sutton書中7-3節

總結

n-step Learning在實務上並沒有特別實用，我們就不再深入討論。但透過n-step Learning，能讓我們稍微理解TD Learning與Monte Carlo之間的關係。Monte Carlo其實就是一種擴展後的TD Learning。