這個方法將變數下的資料放進N個區間,且每個區間的資料數量是相同的。這是一個較好的方法,假如我們想要偏態分布資料能平均分布於各個區間。基本上,我們使用四分位數(quartiles)或百分位數(percentiles)來決定區間的界線。至於需要幾個區間,並沒有嚴格的規則。
將資料平均分布於各個區間,可能會改善機器學習演算法的效果,但另一方面也可能會破壞變數與標籤之間的關係。
我們可以使用pandas或scikit-learn 來對資料做分隔。
以 Kaggle 的 Titanic 資料集中的"年齡"變數來說明:
Rec-No |Survived| Age | Fare
------------- | -------------
0 | 0 | 22.0| 7.2500
1 | 1 | 38.0 | 71.2833
2 | 1 | 26.0 | 7.9250
3| 1 | 35.0 | 53.1000
4 | 0 | 35.0| 8.0500
.. | ... | ...| ...
886 | 0 | 27.0| 13.0000
887 | 1| 19.0| 30.0000
888 | 0| NaN| 23.4500
889 | 1| 26.0| 30.0000
890 | 0 | 32.0| 7.7500
(1)使用pandas
使用pandas的qcut(quantile cut)函數,將資料分隔成10個區間。
retbins值=True,表示我們要程式記住區間(intervals)的界線值,所以我們才能用這些值來分隔測試資料集。
X_train['age_disc'], intervals = pd.qcut(
X_train['Age'], 10, labels=None, retbins=True, precision=3, duplicates='raise')
檢視區間的界線值
intervals
array([ 0.42, 12.2 , 19. , 22. , 26. , 29. , 32. , 36. , 41. ,
50. , 80. ])
查看分隔後和分隔前的年齡資料
print(X_train[['Age', 'age_disc']].head(10))
/| Age | age_disc
------------- | -------------
857 | 51.0 | (50.0, 80.0]
52 | 49.0 | (41.0, 50.0]
386 | 1.0 | (0.419, 12.2]
124| 54.0 | (50.0, 80.0]
578 | 19.0 | (12.2, 19.0]
549| 8.0 | (0.419, 12.2]
118| 24.0| (22.0, 26.0]
12 | 20.0 | (19.0, 22.0]
157 | 30.0 | (29.0, 32.0]
127| 24.0 | (22.0, 26.0]
檢查每個區間資料的數目
X_train['age_disc'].value_counts()
| (32.0, 36.0] | 76 |
|---|---|
| (22.0, 26.0] | 71 |
| (41.0, 50.0] | 70 |
| (12.2, 19.0] | 70 |
| (0.419, 12.2] | 63 |
| (19.0, 22.0] | 61 |
| (26.0, 29.0] | 60 |
| (50.0, 80.0] | 54 |
| (29.0, 32.0] | 52 |
| (36.0, 41.0] | 46 |
| Name: age_disc, dtype: int64 |
檢視每個區間資料的數目占全體資料的比率
X_train['age_disc'].value_counts()/ len(X_train)
| (32.0, 36.0] | 0.121990 |
|---|---|
| (22.0, 26.0] | 0.113965 |
| (41.0, 50.0] | 0.112360 |
| (12.2, 19.0] | 0.112360 |
| (0.419, 12.2] | 0.101124 |
| (19.0, 22.0] | 0.097913 |
| (26.0, 29.0] | 0.096308 |
| (50.0, 80.0] | 0.086677 |
| (29.0, 32.0] | 0.083467 |
| (36.0, 41.0] | 0.073836 |
| Name: age_disc, dtype: float64 |
使用pandas的**cut()**函數(不是qcut()函數),及分隔訓練集所得到的區間界線值,來分隔測試資料集。
X_test['age_disc'] = pd.cut(x = X_test['Age'], bins=intervals)
X_test['age_disc'].value_counts() / len(X_test)
X_test.head()
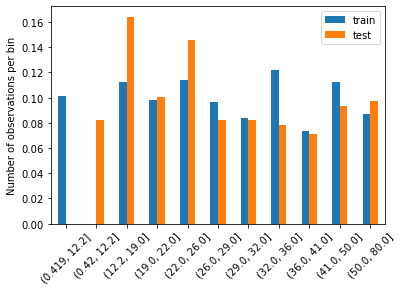
比較訓練集和測試集的分隔後的資料分布情形-各區間資料的數目占全體資料的比率。
t1 = X_train['age_disc'].value_counts() / len(X_train)
t2 = X_test['age_disc'].value_counts() / len(X_test)
# concatenate aggregated views
tmp = pd.concat([t1, t2], axis=1)
tmp.columns = ['train', 'test']
# plot
tmp.plot.bar()
plt.xticks(rotation=45)
plt.ylabel('Number of observations per bin')
(2)使用scikit-learn
disc = KBinsDiscretizer(n_bins=10, encode='ordinal', strategy='quantile')
disc.fit(X_train[['Age']])
KBinsDiscretizer(encode='ordinal', n_bins=10)
各區間的界線值儲存在disc.bin_edges 中
disc.bin_edges_
array([array([ 0.42, 12.2 , 19. , 22. , 26. , 29. , 32. , 36. , 41. ,
50. , 80. ])], dtype=object)
分隔訓練資料集
train_t = disc.transform(X_train[['Age']])
train_t = pd.DataFrame(train_t, columns = ['Age'])
train_t.head()
| / | Age |
|---|---|
| 0 | 9.0 |
| 1 | 8.0 |
| 2 | 0.0 |
| 3 | 9.0 |
| 4 | 2.0 |
分隔測試資料集
test_t = disc.transform(X_test[['Age']])
test_t = pd.DataFrame(test_t, columns = ['Age'])
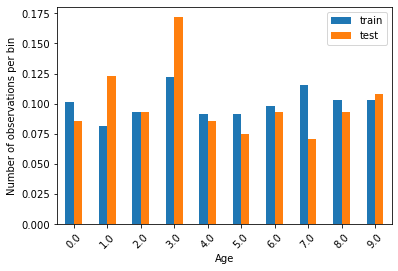
比較訓練集和測試集的區間資料分布情形-各區間資料的數目占全體資料的比率。
t1 = train_t.groupby(['Age'])['Age'].count() / len(train_t)
t2 = test_t.groupby(['Age'])['Age'].count() / len(test_t)
tmp = pd.concat([t1, t2], axis=1)
tmp.columns = ['train', 'test']
tmp.plot.bar()
plt.xticks(rotation=45)
plt.ylabel('Number of observations per bin')
分隔前和分隔後的資料的比較:
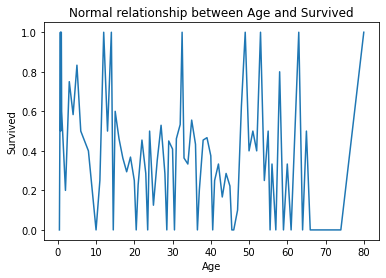
原始資料中年齡和存活率的比較圖
fig = plt.figure()
fig = X_train.groupby(['Age'])['Survived'].mean().plot()
fig.set_title('Normal relationship between Age and Survived')
fig.set_ylabel('Survived')
做分隔後的資料中年齡和存活率的比較圖
fig = plt.figure()
fig = X_train.groupby(['Age_disc'])['Survived'].mean().plot(figsize=(12,6))
fig.set_title('Normal relationship between variable and target')
fig.set_ylabel('Survived')
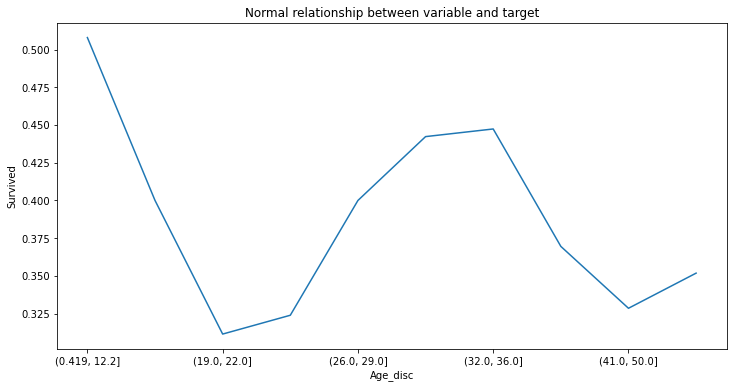
比較上述兩個圖,分隔後的圖更清楚的看出年齡和存活率的關係,十八歲以下和三十歲出頭最可能存活下來,二十歲至三十歲和大於三十五歲者最不可能存活下來。
