今天要講的是 Dynamic Programming。

Dynamic Programming 在某種程度上來說，也是一種把大問題切成小問題的演算法。但和 Divide and Conquer 不同的是，Divide and Conquer 是從上往下，但 Dynamic Programming 卻是反過來，從下算到上。

想像一下，假設今天要算的是費波那契數列（從 0 和 1 開始，後面的數字依序為前兩個數字相加），我們可以先 Divide，把 f(n) 拆成 f(n-1) + f(n-2)，然後一直拆到 f(1) 和 f(2) 為止，最後再用 Conquer 加起來。例如

f(1) = 0
f(2) = 1

f(7) 
= f(6) + f(5) 
= f(5) + f(4) + f(4) + f(3)
= f(4) + f(3) + f(3) + f(2) +  f(3) + f(2) + f(2) + f(1) 
= ...

可以看到，我們要一直拆重複的數字，這些動作非常繁瑣。但是，假如我們在拆完一個數字後，就把它記下來，需要的時候再拿表查詢並直接用，不是就方便多了嗎。

這是 Dynamic Programming 基礎的概念，假設今天 問題 a 可以分解成 問題 b * 問題 c * 問題 d，那我們就先解 問題 b，然後解 問題 b * 問題 c，最後算出 問題 b * 問題 c * 問題 d = 問題 a。

聽起來有點繞口對吧，但畫圖太麻煩，這邊指路一個矩陣相乘實例的好懂課程，如果有線代基礎可以直接看，不然花十分鐘搜尋一下矩陣相乘規則再進入也可以。有興趣可以整個看完，或是跳到 28:00 開始是實例介紹，真的神乎奇技。

最後補充一下，Dynamic Programming 的使用是有限制的。這個算法是把大問題拆成小問題，但大問題的最佳解必須也是小問題的最佳解，不然就無法成立。所以在使用前，可以用反證法評估一下。

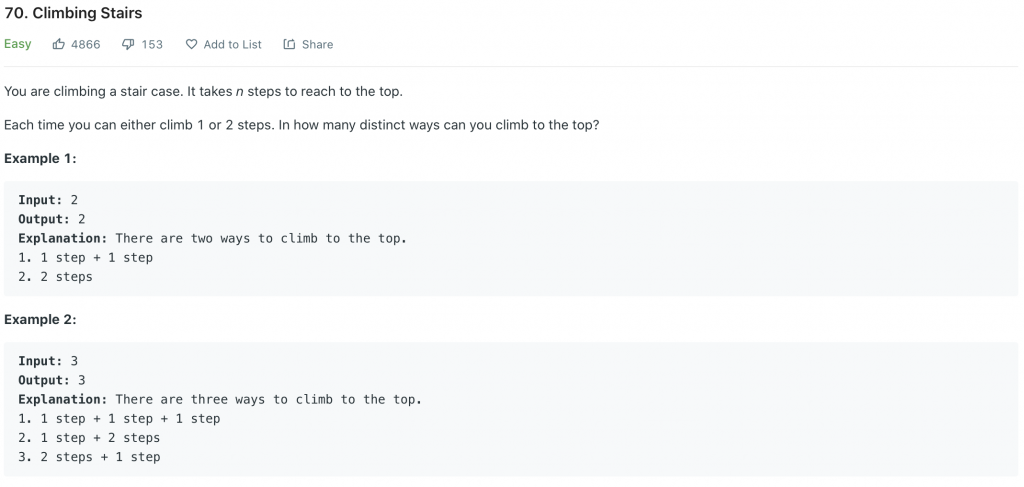
好的，認清自我不要幻想從 easy 做起。今天看的是爬樓梯問題，假設今天要爬上第 n 階，每次可以走一階或跳兩階，那總共有幾種爬樓梯的方式呢。爬上第 n 階時，前一步不是在 n-1 就是 n-2，只有這兩種可能，所以可能性就會是爬到 n-1 和 n-2 的加總啦。

// javascript
var climbStairs = function(n) {
  let arr = [0,1,2]
  for(let i = 3; i <= n; i ++) {
    arr[i] = arr[i-1] + arr[i-2]
  }
  return arr[n]
}

// 附帶熟悉一下 c++ 語法，為什麼這個 runtime 是 0 怎麼回事
class Solution {
public:
  int climbStairs(int n) {
    if(n <= 2)
      return n;
      
    int arr[n];
    
    arr[0] = 1;
    arr[1] = 2;
    for(int i = 2; i < n; i ++) {
        arr[i] = arr[i-1] + arr[i-2];
    }
    return arr[n-1];
  }
};