通常數學不耐症
是因為公式中含有大量的符號
要克服這個
我認為最好的方法就是實例練習

假設我們現在想知道國中生罹患中二病的機率
抽查了 50 個班級，每班 10 個學生
結果如下：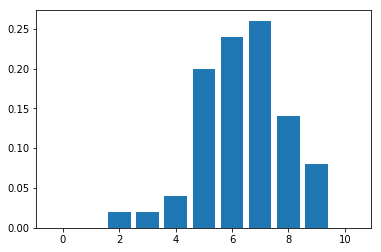

假設每個學生罹患中二病的情況是獨立事件且罹患機率為 true_pi
我們可以假設我們所觀察的現象服從二項分配

我們現在猜測兩個機率 pred_pi_1 = 0.4, pred_pi_2 = 0.5
那我們要選擇哪一個模型比較好呢

首先分別看兩個猜測的分配與觀察到的圖形差異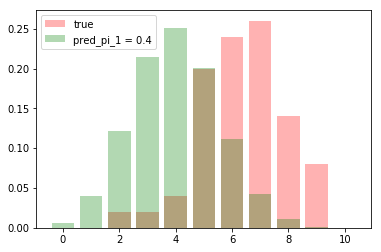

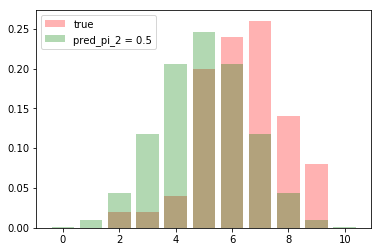
然後分別看分布的機率
prob_true = [0.0, 0.0, 0.02, 0.02, 0.04, 0.2, 0.24, 0.26, 0.14, 0.08, 0.0]
prob_pred_1 = [0.01, 0.04, 0.12, 0.21, 0.25, 0.2 , 0.11, 0.04, 0.01, 0.0, 0.0]
prob_pred_2 = [0.0, 0.01, 0.04, 0.12, 0.21, 0.25, 0.21, 0.12, 0.04, 0.01, 0.0]

利用這些分布分別去計算 KL 散度
以 prob_true 與 prob_pred_1 為例

prob_pred_1, prob_pred_2 中雖有些呈現是 0
但那是因為我只取到小數點第 2 位的結果，故其真實值非0
所以若在真實計算中，分母都是非 0

若遇到以下情況有約定值(可利用微積分驗證)：

類似作法可做出
比較兩者後可知
參數的選擇 pi 應選 0.5 較好(KL散度越小越好)

執行程式碼如下

import random
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import entropy
import math

# 選擇數的公式
def nCr(n, r):
    f = math.factorial
    return f(n) / f(r) / f(n-r)

# 二項分配
def binomial_distribution(n, r, pi):
    return nCr(n, r)*(pi**r)*(1-pi)**(n-r)
    
# 真實機率
true_pi = 0.587

# 創造樣本
sample = [sum(1 for i in range(11) if random.random()<true_pi) for j in range(50)]
prob_obs = [sample.count(i)/50 for i in range(11)]

# 畫出觀察到的分配
plt.bar(np.arange(11), prob_obs)
plt.show()

# 猜測 pi，並依此計算機率
pred_pi_1 = 0.4
bi_dist_1 = [binomial_distribution(n = 10, r = r, pi = pred_pi_1) for r in range(11)]

pred_pi_2 = 0.5
bi_dist_2 = [binomial_distribution(n = 10, r = r, pi = pred_pi_2) for r in range(11)]

# 從圖形上看 true, pred 差異
plt.bar(np.arange(11), prob_obs, alpha = 0.3, color = 'red', label = 'true')
plt.bar(np.arange(11), bi_dist_1, alpha = 0.3, color = 'green', label = 'pred_pi_1 = 0.4')
plt.legend()
plt.show()

plt.bar(np.arange(11), prob_obs, alpha = 0.3, color = 'red', label = 'true')
plt.bar(np.arange(11), bi_dist_2, alpha = 0.3, color = 'green', label = 'pred_pi_2 = 0.5')
plt.legend()
plt.show()

# 計算 KL
# entropy(pk, qk=None, base=None, axis=0) : if qk = None, then compute entropy; if not None, compute KL
print('KL(true, pred_1) = ', entropy(prob_obs, bi_dist_1))
print('KL(true, pred_2) = ', entropy(prob_obs, bi_dist_2))