上次講到用 P 的等價類去逼近一個樣本子集 X
仔細想想，P 的等價類中的每個集合其實也是個樣本子集
所以如果現在有一個目標特徵子集 Q
則 Q 的等價類( U/Q )中的每個集合都是個樣本子集
那如何用 P 去逼近它呢？

上次說 X 用 P 做逼近就像 X 用 P 做組合
等價類之間的逼近，也像是 U/Q 用 U/P 做組合
也就是說 P 是否可以把 Q 細分

就跟上次一樣我們用一個粗糙集去逼近它
那我們會需要一個內逼近和外逼近
於是定義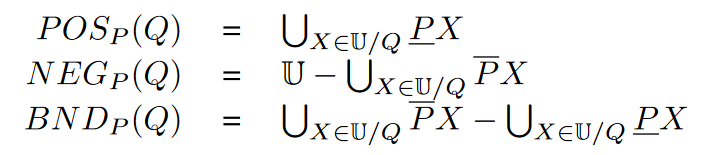

一個一個看
：它把所有可以內逼近 Q 的等價類的元素收集起來
這代表如果這個集合非空，則裡面的元素在特徵 Q 之下可被 P 細分類

：它用樣本空間 U 扣掉 所有可以外逼近 Q 的等價類的元素
這代表如果這個集合非空，則裡面的元素對 Q 不可分類

所以想像成 POS 代表內部、NEG 代表外部
則 就是 宇集U 扣掉外部 再扣掉內部
想像一下就可以知道它是在講邊界

直接用它的例子~

如果現在取 P = {b, c}, Q = {e}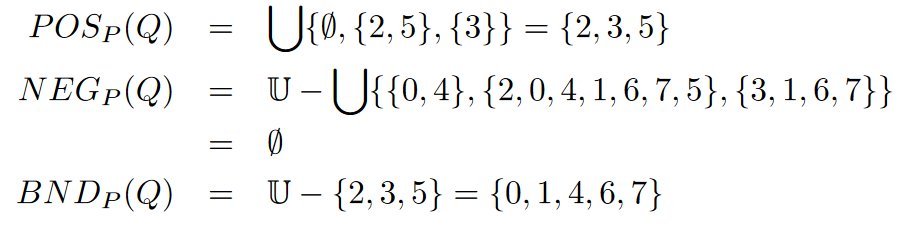

POS = {2, 3, 5} 中的元素表示他們在特徵 Q 之下可以被 P 細分

樣本|b|c|e
--|--|--|
2|R|R|S
3|S|R|T
5|T|S|S

可以看到在特徵 Q = {e} 之下，
{2, 3, 5} 可以完全被 P = {b, c} 細分類