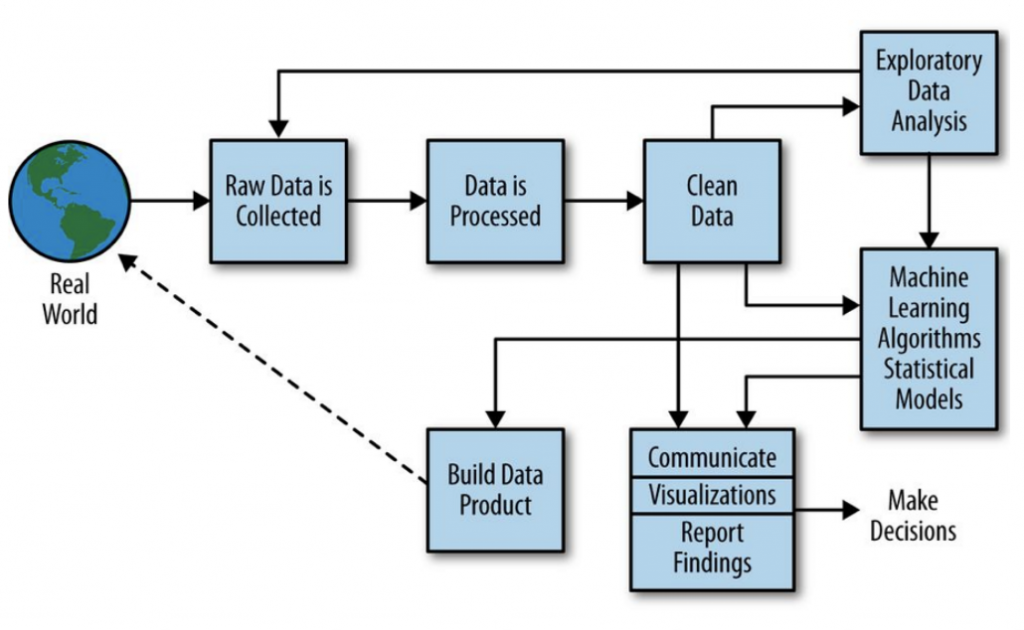
那麼，資料科學家都在做哪些事？我們來看看資料科學處理的流程，並簡介一些統計的原則及運用：

1. Raw Data is Collected（from Real World）：在真實世界中收集原始資料，不論是哪種行業，在最源頭資料庫建構的資源及做法是很關鍵的，如在不知道哪種資料有用的狀況下，製造業要廣布 sensor、醫療業要有高品質的病歷
2. Data is Processed and Cleaned：資料整理、清理，排除異常資料，視資料數量及型態做補值
3. Exploratory Data Analysis (EDA)：探索式分析，確認資料特性
4. Machine Learning Algorithms, Statistical Models：瞭解資料後，選用合適的統計或機器學習的方法來試試看能否找到關聯性或有意義的結果（模型配適）
5. Communicate / Visualizations / Report Findings / Build Data Product：如果結果相當不錯，可視覺化展現、商業應用
   
   圖片來源：Doing Data Science (O’Neil and Schutt)

統計圖表的目的是表示真相、解釋事實、讓我們容易瞭解，在製作的過程原則是要傳達正確的資訊、避免花俏、指標明確不要太多，也要注意 (1) 有沒有根據目的及資料特性選擇適合的統計圖；(2) 刻度及範圍選擇不對會造成視覺的誤導；(3) 離群值影響圖表特性的敏感度、找出影響分析較多的數值並忽略掉；(4) 重疊度 (sample size) 資料量多時在視覺呈現上會有點難看出圖表上的微觀與巨觀差異，比如直方圖建議要調間隔、Zoom in 去仔細觀察。巨量資料是否能解決我們的問題，要先花時間及結合經驗確認要挑選哪些合適的工具去做分析，否則容易誤判。

Excel 中有許多 Visualize Data 的工具，在「插入圖表中」如果想看資料間的關係可用散佈圖（Scatter Chart）、比例則用圓餅圖（Pei Chart）、不同組合資料集要比較統計概況如全距及變異用盒鬚圖（Box and Whisker, Box Plot, 箱子中間是中位數、兩端是 25 & 75 分位數 Q1 與 Q3, 而 Q3-Q1 的值稱為 IQR, Q1 - 1.25IQR = Minimum, Q3 + 1.25IQR = Maximum, 超過最小與最大值則為離群值 Outliers）、資料類別型變數的類別數、分佈與走勢可用直方圖（Histogram）。統計關心的三個指標有 [1] 集中量數（Measures of Central Tendency） - 算數平均數（Mean）、中位數（Median），比如我們會想知道一個班級的考試平均分數、50% 的學生考多少分、最多學生考幾分，或是國民所得的平均和中位數因為貧富分布的關係差很多；[2] 分散程度的變異數（Measures of Variance）- 一般會用常態分佈去看資料，正負 1 個標準差大約涵蓋了 68% 的範圍資料、2 個標準差約 95%、3 個標準差則約 99.7%，所以我們常說 3 個標準差以外只佔了千分之三以內的機率；[3] 樣本數，每個圖表可能足以展現某些面向、但無法彰顯其他面向，因而有各自的限制，例如 Box Plot 雖能顯示分佈但難以表達出樣本數，量太少時看起來可能沒什麼變異、很集中而無法真實呈現，樣本數要夠多才具有代表性。如果我們想對資料集有充分瞭解，可能要多畫幾張不一樣的圖、互做搭配。

相關敘述統計量當中，以常態分佈為基準，去評估 (1) 峰態 - 大於 3 稱為高峽峰（數字密集）、等於 3 為常態峰、小於 3 為低闊峰；(2) 偏態（兩側是否對稱） - 大於 0 為右偏、等於 0 為對稱分配、小於 0 為左偏。

偽相關性（Spurious correlations）是另一個讓資料分析者困擾的情形，比如我們看到兩者有相關，但這個相關性似是而非、不太能合理解釋。比如下圖的統計圖表讓我們看到「跌到池子裡溺死的人數」與「尼可拉斯凱吉參與演出電影的數量」呈高度相關，不過二者有沒有真正的意義就需要進一步確認並解釋了，而不能解釋不見得不能執行，這也是有趣的地方。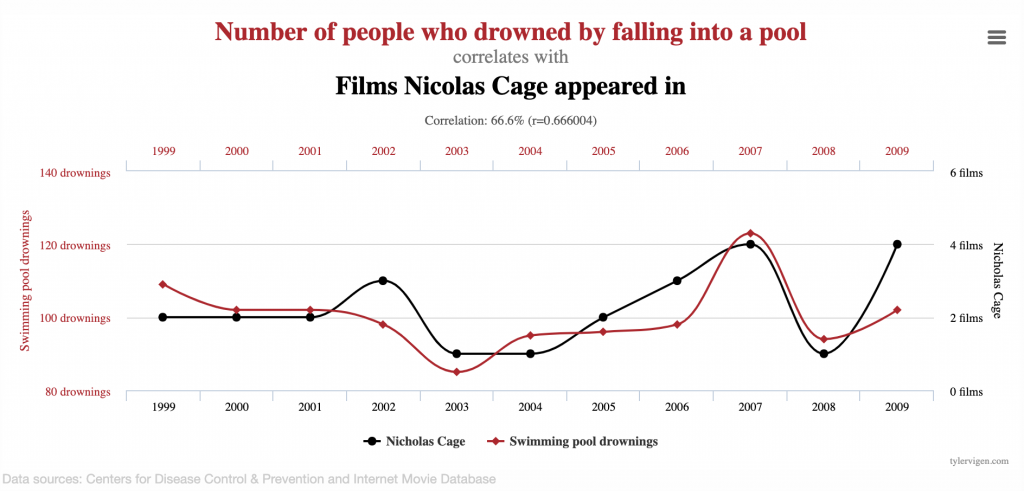

圖片來源：https://www.tylervigen.com/spurious-correlations

如果我們想看單一樣本平均（如手機平均銷售額）在時間軸上的不同時間點（如去年與今年）有沒有差異，選用 one-sample t-test；而比較不同群體的平均（如手機及平板平均銷售額）也選用 t-test 比較是否有差異。而多個（三個以上）群體的比較則用 ANOVA 分析，比如分析百貨門市的手機、獨立店面的手機、百貨門市的平板、獨立門市的平板平均銷售額是否有相關。

當我們想利用統計的方法做預測，從不同的變數、過往的銷售資料來預測未來的銷售可能，則選用回歸分析（Regression），比如利用平假日、門市地點、行銷方式、價格的資料來對應銷售數量。根據資料型態及特性，選用不同性質的回歸（如線性或非線性）來做分析。這和資料的數量沒有太大關係，只要資料存在高度相關便能跑出來，可參照 R^2（資料的適配度）。

那麼，資料科學家最常使用哪些演算法？根據 KDnuggets 2016 做的調查，Regression、Clustering（客人要分成哪幾群）、Decision Tree/Rules、Visualization 是前四大最常被使用的，而因為我們經常需要做預測，迴歸被列在第一名就不那麼例外了。

圖片來源：https://www.kdnuggets.com/2016/09/poll-algorithms-used-data-scientists.html

希望這些資訊能幫助我們認識基本資料分析方法、每種方法怎麼用、怎麼用對方法，在應用上如果具有 Domain Know-How 能大大有助於我們決定要收集哪些資料，再用不同角度運用資料回答並驗證初始的問題及假設，相信我們都能夠為資料科學貢獻一份心力！