哈囉大家好，我是橘白卯咪，歡迎大家來看看我能不能撐過30天

今天要來談談我們用來萃取行為特徵的主成分分析法

主成份分析(Principal Components Analysis, PCA) 是一種降低資料維度的方法，用主成分特徵來解釋變異。在機器學習上用來降低資料維度，避免維度詛咒，並且可用於特徵萃取、降低雜訊；在統計學上用來萃取變數中的主要成分。

看完上面這幾行字，如果現在的你跟當時剛接觸PCA這個名詞的我一樣，覺得明明是中文卻看不太懂
於是你去google了一下 wiki
嗯好的， 我不懂中文，數學也不好，窩4個廢5

在不講任何數學公式的狀況下，我認為PCA主要有兩個重點

投影與旋轉

配張我覺得好懂的圖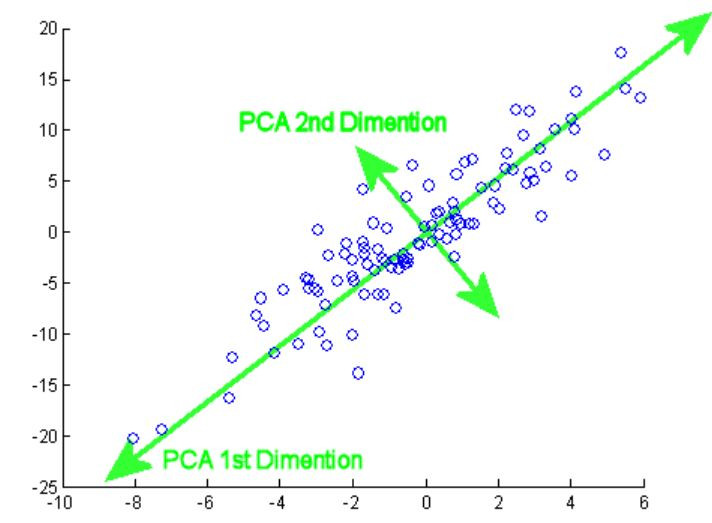

出處
首先想像圖中的藍色點點(資料點)都是一顆顆球體，球池裡會看到的球

投影 如字面上所述，拿一盞燈，以圖中最長的綠線為牆面，向這些球球照過去~
會得到一張充滿這些資料點的平面
圖中最長的綠線和最短的綠線，就是特徵

旋轉，如果以這兩條垂直相交的綠線，當作x、y軸，就需要把這些球球轉一轉
再看哪一些球的x值y值大，就代表這些"特徵的分數高"
這張李宏毅老師的投影片也很好理解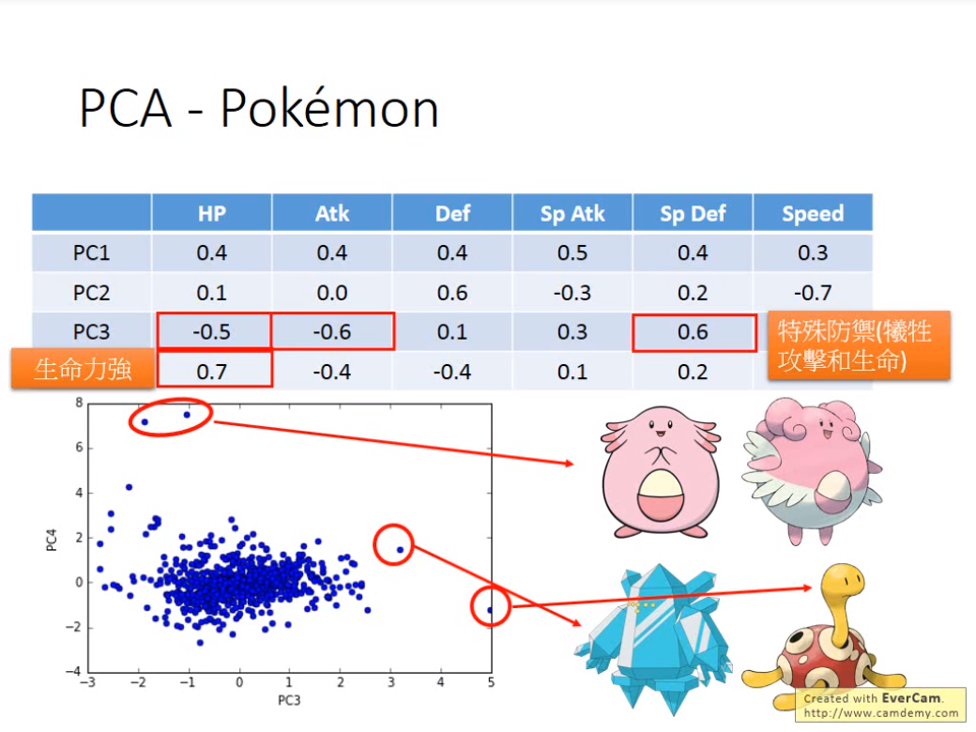

出處
PCA3: 特別防禦為正，血量與攻擊為負，這代表用血量與攻擊來換特別防禦
PCA4: 用攻防來換取高血量，兩者成反比

為了寫這一篇文，真的有努力地找過，對於PCA，有沒有數學少一點又白話的解釋
唯一一篇夠白話的是ptt上的解釋

"對於每一個帥哥的條件,你都可以利用其自變數(身高,腿長,膚質,衣著打扮,衛生習慣)
算得第1主成分和第2主成分的分數
然後以第1主成分當x軸,第2主成分當y軸, 把每個點標在圖上

藉由點的分布及現有的自變數推測, 第1主成分可能是什麼。
所以,假設你看到帥哥的條件=好的,第1主成分分數高,
帥哥的條件=差的,第1主成分分數低,再回去看 帥哥的條件=好的 且 第1主成分分數高的, 大多數是身高高, 腿長, 皮膚好。
帥哥的條件=差的 且 第1主成分分數低的, 大多數是身高矮, 腿短, 皮膚差
接著才可以推測第1主成分 與 身高、腿長、膚質有比較大的關係

簡而言之，PCA在推測什麼因素跟我們的目標有比較大的關係
抱歉寫的很亂
來點參考文章吧

參考文章

這篇是白話解釋加點圖跟公式
這篇的動畫超級精美，看一看或許能比較了解
這篇結合了R語言做解說