正規化的方法：
6.1 Standardisation(標準化)
6.2 Min-Max Scaling
6.3 Maximum Absolute Scaling
6.4 Robust Scaling
6.5 Mean normalisation
6.6 Scaling to unit length

以 Kaggle 的 Titanic 資料集來說明：

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler,RobustScaler,Normalizer
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
%matplotlib inline
# load the numerical variables of the Titanic Dataset
data = pd.read_csv('../input/titanic/train.csv', usecols = ['Pclass', 'Age', 'Fare', 'Survived'])

data.isnull().sum()
X_train, X_test, y_train, y_test = train_test_split(data[['Pclass', 'Age', 'Fare']],
                                                    data.Survived, test_size=0.3,
                                                    random_state=0)
                                                    
X_train.Age.fillna(X_train.Age.median(), inplace=True)
X_test.Age.fillna(X_train.Age.median(), inplace=True)                                           

6.4 Robust Scaling(穩健縮放)

Robust Scaling 是將變數值減掉中位數(median)再除以變數的四分位數間距，四分位數間距是第三四分位數(the 3rd quartile or 75th quantile)減第一四分位數(the 1st quartile or 25th quantile)。這個過程基本上和Min-Max Scaling相似，但它提供了一個較好的範圍給高度偏態分布的資料。縮放後，每個變數間的變異數、最大值、最小值不一樣，也可能改變原始資料分布的型態，不容易受到異常值影響。

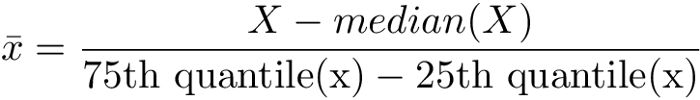
robustscaler = RobustScaler() # create an object
X_train_scaled = robustscaler.fit_transform(X_train)
X_test_scaled = robustscaler.transform(X_test)

6.5 Mean normalization

這個方法是將變數值減掉平均值再除以變數間距，變數間距是變數中的最大值減掉最小值，所以產生一個變數值範圍是-1至1，且以0為中心的資料分布。縮放後，變異數會不同於原始變異數，也可能改變原始資料分布的型態，但會保留異常值。

使用pandas：

means = X_train.mean(axis = 0)
max_min = X_train.max(axis = 0) - X_train.min(axis = 0)

X_train_scaled = (X_train - means) / max_min
X_test_scaled = (X_test - means) / max_min

使用scikit-learn：

scaler_mean = StandardScaler(with_mean=True, with_std=False)
scaler_minmax = RobustScaler(with_centering=False,
                             with_scaling=True,
                             quantile_range=(0, 100))
scaler_mean.fit(X_train)
scaler_minmax.fit(X_train)

X_train_scaled = scaler_minmax.transform(scaler_mean.transform(X_train))
X_test_scaled = scaler_minmax.transform(scaler_mean.transform(X_test))

6.6 Scaling to unit length

這個方法是將變數縮放至一個單位長度(unit length)，我們稱這個單位為向量，它的長度是1。他的公式是將變數值除以變數的歐幾里得距離(Euclidean distance)或曼哈頓距離(Manhattan distance)。這個方法易受到異常值影響，適用於文字分類和clustering。

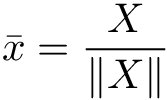
歐幾里得距離(Euclidean distance)又稱為 L2 norm 或 L2 distance，公式如下：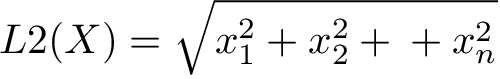

曼哈頓距離(Manhattan distance)又稱為 L1 norm 或 L1 distance，公式如下：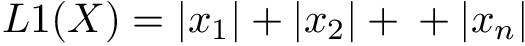

歐幾里得距離將變數值平方，所以異常值會占有較大權重(heavier weight)，因此如果有異常值，建議使用L2 norm。

scaler = Normalizer(norm='l1')

scaler.fit(X_train)

X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)