從昨天的內容我們可以知道損失函數是用來計算模型預測值與預期輸出之間的相似程度，並在訓練過程中需要將預測值與輸出的相似程度最小化，接下來我要介紹是常用的損失函數:MSE和MAE。
常用損失函數: 均方誤差(Mean square error，MSE)和平均絕對值誤差(Mean absolute error，MAE)
在機器學習和統計學中常被用在回歸上的損失函數就是均方誤差MSE)，那怎麼會有「均方值」這個字，我提到都是預測值與真實值之間的差異，這差異不是只是一個值嗎?因為資料有可能不只有一筆，有可能有一百筆甚至一千萬筆，所以需要計算這所有資料的平均值，但平均值計算的差值內有正有負，直接相加會有問題。
比如兩筆資料y1=0, y2=1結果模型預測ŷ1=100，ŷ2=-99。
loss1=y1- ŷ1=0–100=-100
loss2=y2- ŷ2=1-(-99)=100
loss1+ loss2=-100+100=0
預測差值等於0。
但這樣合理嗎?一定不合理阿。
所以加個平方值都是正數，那預測值和實際值的差異就出來了。

下圖是我參考網路上MSE和MAE的差異，說明了假設實際值為0，預測值為-10~10，可以發現平方的loss很大(紅色軸)，絕對值的loss相對小很多(藍色軸)，而且平方的loss變化比較曲線，絕對值的loss比較線性(V字)。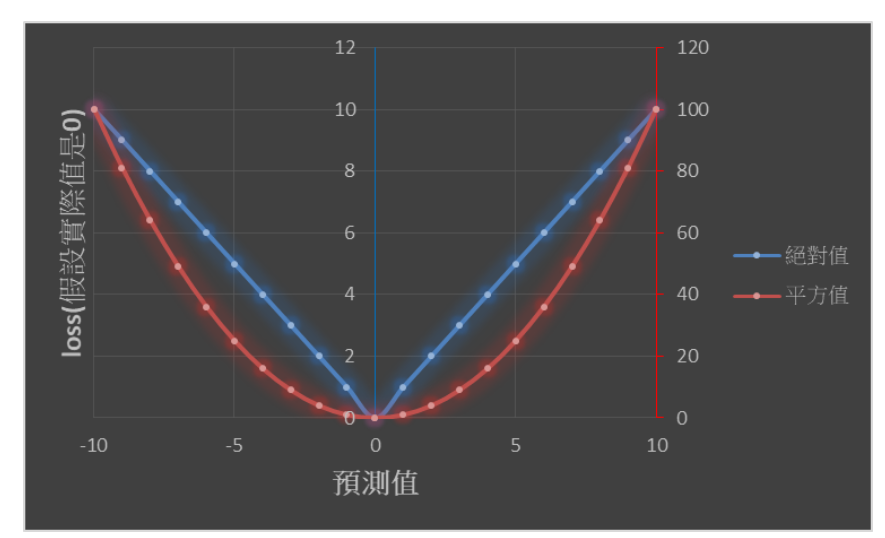

今天我看了很多關於損失函數的文章發現，其實平方跟絕對值的貢獻不是在找解部分，因為大多數的資料頂多一兩個outlier，如果樣本數多一點，outlier根本不太影響，所以這兩個方法基本上都在正規化參數上比較常用來比較差異。
L1 Regularization其實是norm-1正規化→絕對值。
L2 Regularization其實是norm-2正規化→平方值。
結論
MAE對outlier比較有用，但因為微分不連續(剛剛的例子在x=0時，MAE函數就不可以微分)，因此可能在執行時容易出錯，MSE對outlier較敏感，但在求解時，比較容易找到穩定的解。
最後，梯度更新法分很多種，有一開始提到的梯度下降法，是一次使用全部的訓練資料計算損失的函數的梯度，並更新一次權重，如果要更新N 次就必須訓練資料N遍，也讓這個方法變的很沒有效率。因此出現了(隨機梯度下降法)，透過一次計算一個批次資料的梯度並更新一次權重，大大的降低更新的時間，當然還有很多的改良方法，例如Momentum、AdaGrad、Adam都有各自擅長的地方。
參考
https://medium.com/@chih.sheng.huang821/%E6%A9%9F%E5%99%A8-%E6%B7%B1%E5%BA%A6%E5%AD%B8%E7%BF%92-%E5%9F%BA%E7%A4%8E%E4%BB%8B%E7%B4%B9-%E6%90%8D%E5%A4%B1%E5%87%BD%E6%95%B8-loss-function-2dcac5ebb6cb