Day 27 — B+樹與關聯式資料庫

昨天我們說，建立索引可以減少空間，讓我們找到資料庫中資料儲存在磁碟上面的位置。問題是，索引這麼多，要怎麼才能快速有效率地找到索引呢?這時候就要來介紹關聯式資料庫最常使用的 B+ 樹。這邊針對樹的資料結構我不會仔細討論，但注意的是，他不是 二元樹 (Binary Tree)。他是 B+ Tree。

B+ 樹 (旋轉過後*) 大概長這樣 (圖片取自上課講義)

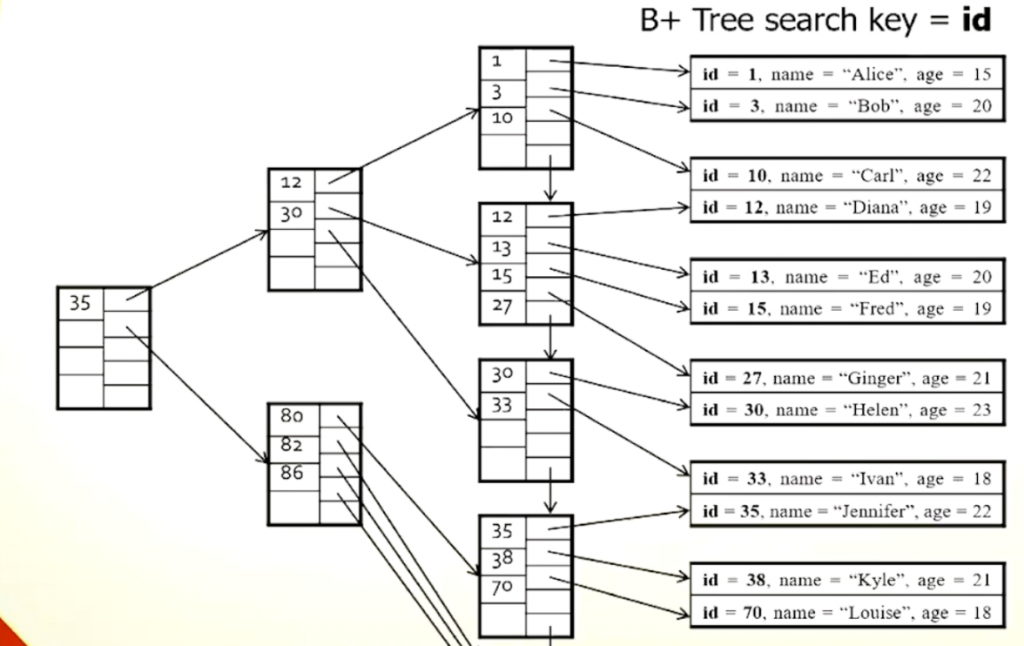
(*一般來說 樹應該是根在上葉在下，這邊我們讓他向左轉90度，比較好看。)

我們快速解釋做邊的格子比紹的是數值，右邊的格子存放的是指向下一個節點或是資料的記憶體位置。

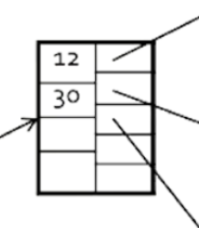
B+樹的根很直覺，有幾個索引。比這個索引小就往上走，比索引大就往下走。所以30 會在35的左邊。中間的節點一樣，會有各自的數值根記憶體儲存空間，B+樹最特別的是它的葉子。

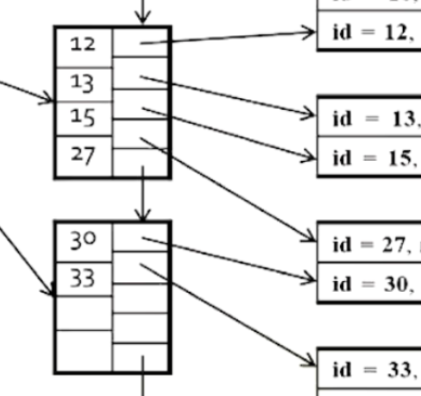
跟一般樹不同的地方是，它的葉子是串再一起的，也就是每個葉字走到底可以走靠下一片葉子。每一便葉子裡面的記憶體位子則是指向磁碟中的資料。

現在這棵樹是依照資料的 ID 編號做編排的。所以當我寫下

Select * From People Where id=27;

我們沿著這個B+樹，按照下面的順序: 我要找的是27，27比35小，所以我往上走；27比12大比30小所以我走到30指向的節點。這個節點帶我到這棵樹的葉子，我就在這個葉子裡面找到27 指向 磁碟中的資料位置。

那為什麼要那個箭頭呢?

Select * From People Where id>27;

我們透過一樣的方式找到了相同的葉子，這時候因為我找的是大於27的所有資料27的所有資料，所以，我就可以直接透過葉子跟葉子之間的串聯，按照順序把所有符合這個條件的資料，逐筆列出。

B+樹的另外一個優點是，有的時候這筆資料根本就不存在資料庫裡面，這時候，我們透過索引可以提前在相對應的葉子中確定沒有符合我們在搜尋的資料。

新增資料

圖片取自網路資料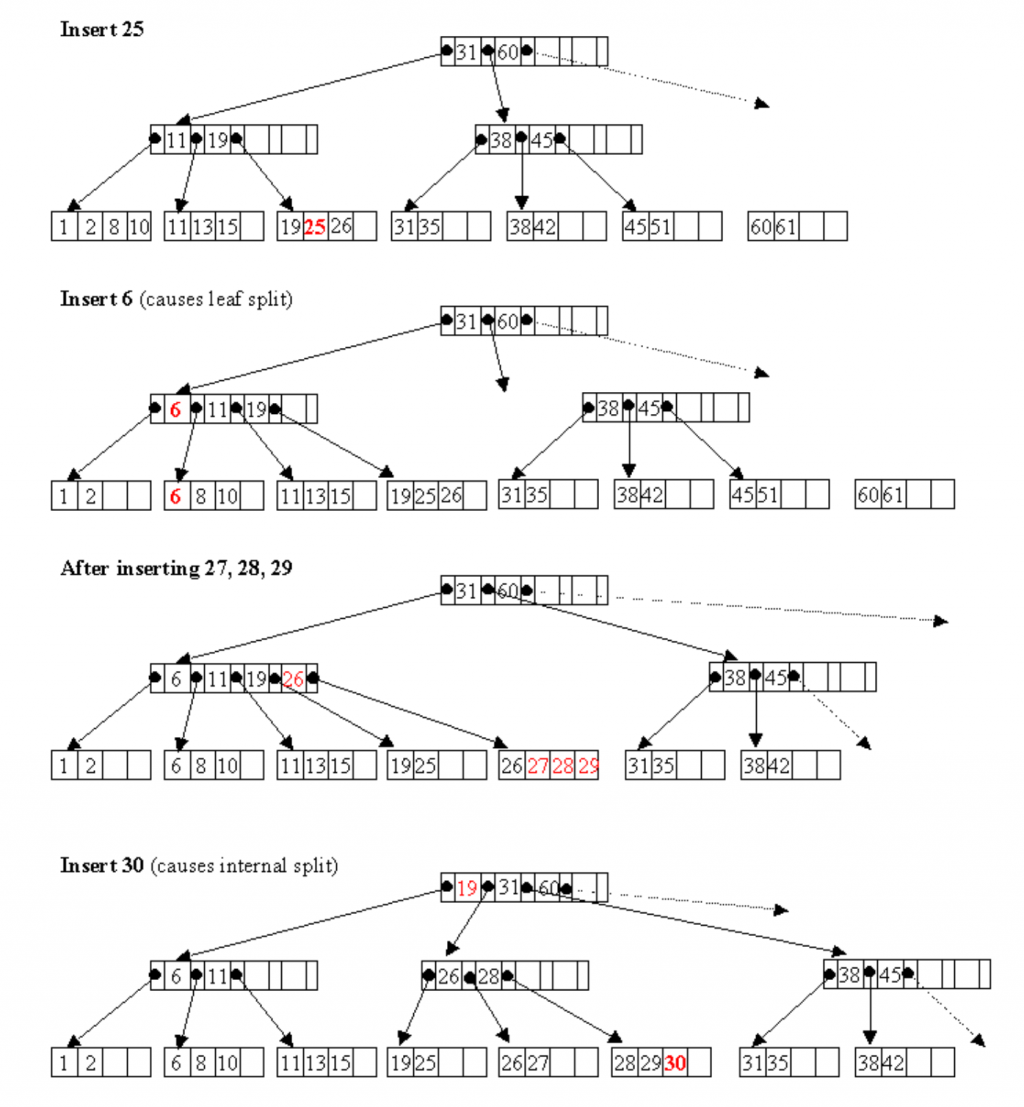

這邊我們來開一連串的資料插入過程，首先在最上面的那個B+樹中，我們插入了25。插入過程跟一般的樹狀資料結構相同。我們要先做搜尋的動作: 25比31還要小往左邊的節點走；25比19還要來得大所以往19右邊的節點走；來到葉子的時候就放置在比19大比26小的空間之中。

接下來我們要插入6。這時候6比31還要小往左邊走；6比11還要小所以我們要把6放到左邊的葉子裡面。這時候發現左邊葉子滿了，所以我們被迫把這個葉子分割成兩個新的葉子，並往上把6加到節點中的索引。相同的下面兩個步驟，加入27 28 29會造成原本在19 25 26的葉子滿出來，所以B+樹創造了一個分割，同時我們會發現左邊 6 11 19 26的節點也滿了，所以在下面插入30的時候中間的這個節點也會自動分割。

B+樹還有很多很有趣的特性和可以操作的行為，例如說他可以再刪除過後重新檢視節點的分布，把比較滿的節點資訊轉移到比較少資訊的節點上面 (我們稱之為旋轉)。

B+樹小資訊

儲存空間: O(n)，n 為資料數量
查找速度: O(log n)，n 為資料數量
插入速度: O(log n)，n 為資料數量
刪除速度: O(log n)，n 為資料數量