前面幾篇介紹了推論統計的一些基礎，
也介紹了常態分配、Z檢定、t分配還有t檢定。
其中Z檢定只能處理單一樣本的檢定，
而t檢定是可以處理單一或是兩個樣本的檢定。
那萬一我們的實驗設計中，一個操作變因有不止兩個條件怎麼辦？
這種時候就要出動ANOVA啦！

ANOVA的全名是Analysis of Variance，
中文可以翻作變異數分析。
雖然名為變異數分析，但他跟之前提到的檢定們一樣，
都是專注在平均數的差異喔（先前好像沒有特別指出）。

ANOVA的核心概念是去看樣本平均數之間的差異，
有多少是來自於樣本的差異，有多少是來自於操作變因的影響。

比如說我們有A組的人看AI推薦的文章，B組的人看隨機的文章，
然後針對有用度打分數。
A組跟B組的差距會有兩種來源，
一個是有沒有AI造成的差異（操作變因造成的組間變異），
另一個是不同樣人之間的本來就會有差異（個體差異造成的組內變異）。

上面的說明只有兩組，但實務上我們通常會在操作變因有多個，
或者是單一操作變因有至少三個水準（levels，就是有幾個分組），
才會使用ANOVA。

有人可能會好奇說，當有三個水準以上時，
能不能不要用ANOVA，而是使用多次t檢定來做比較？
(像是如果有三個水準A, B, C，那我們能不能A&B做一次，
B&C做一次，A&C再做一次？）
答案其實是可以的，但是我們對應的顯著水準α就必須要做調整，
這件事情的細節我們等下篇討論型一和型二誤差再談～

ANOVA對應的檢定是F檢定，顧名思義F檢定是基於F分配所產生的檢定。
F分配是什麼呢？
還記得t分配是由「自由度（df）」來控制形狀嗎？
F分配其實就是再推廣，由兩個自由度（df1, df2）來控制形狀。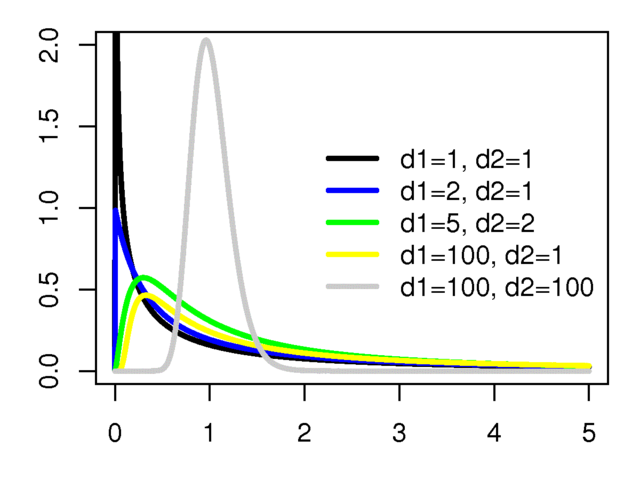

（圖片來源：https://commons.wikimedia.org/wiki/File:F_distributionPDF.png）

在t檢定中，自由度對應的是樣本數（更精確地說是樣本數減一）。
而在F檢定中，自由度1對應的也是樣本數（也就是組內變異），
自由度2則是對應組數（也就是組間變異）。

ANOVA非常的複雜，所以實務上大家大多是拿現有的統計軟體(像SPSS)，
或是用R或Python的一些統計函數庫來寫，
不會真的手算。
但想要了解ANOVA的一些數學計算，我會推薦參考這篇。

還記得實驗設計可以有不只一組操作變項嗎？
這樣的設計ANOVA也可以處理。
如果只有一組操作變項，
那麼我們使用的就是「單因子變異數分析（One-way ANOVA)」。
如果有兩組操作變項，則是
「二因子變異數分析（Two-way ANOVA)」。
二因子變異數分析首先關心的是兩個因子之間的交互作用，
再來才能去看因子分別的影響。

再往上就是「多因子變異數分析（Multiple-way ANOVA)」。
同理，多因子變異數分析可以看各種複雜的交互作用，
但可想而知就是越複雜其實就越難理解，
因此實驗設計必須要小心處理，
才不會設計出過度複雜的實驗，讓分析方法也得跟著變得困難。

另外ANOVA也有分成獨立樣本或是重複樣本的變化版，
東西非常多。如果有興趣了解關於ANOVA更細節的介紹，
強烈推薦這篇：
http://qheroq.blogspot.com/2010/10/analysis-of-variance-anova.html。

那如果ANOVA結果顯著了，我們要怎麼樣知道是哪些組之間有差異呢？
這時候就需要「事後比較分析(Post-hoc Analysis)」
我們就下篇跟型一型二誤差一起再談囉！