歷史是沒有所謂歡樂結局的，只有一個接著一個被渡過的危機時刻。

-- 以薩·艾西莫夫, 諸神自身

-- 0307

進了城裡。卻發現整個城市相當相當的暗，就像夜晚在忽然間降臨了一般。我點起了火把，但看起來什麼都沒有，就像城牆包起來的一大塊區域而己，雖然一眼看不到城牆究竟延伸到哪裡去。

-- 0315

我在城裡晃蕩了一陣子，發現跟城門的情況一樣，當靠近某些地點的時候，會浮現某些像是建築的輪廓來。但是有些看起來比較清晰，就些就只是… 輪廓而己。

我也發現有些建築上都會有些…記號，很多是符號，有些是字。我試著去把那些記號跟建築的位置還有情況對應起來。<> 的建築顏色有點淺，<*> 更淺了。<$> 比前一個深一點點。再過去一點有個過不去的區域，像是非常透明的牆，真不知道那是什麼。

孩子能帶出門之後，感覺他對很多東西很好奇啊。應該要多花點時間帶他去亂晃的，我很喜歡跟他牽手走在路上的那些時間。

-- 0322

我發現其中一棟建築當我走到前面的時候，浮現的樣子非常的…具體，遠比其它的都清楚很多。門楣上畫的標誌是： ->

也許可以看看要怎麼進去。

-- 0403

門上沒有手把，但是有個像是缺口的東西。上方寫著 -> a，我找到地上的數字放一個進去。文字暗下，出現另一個 -> Integer。

重覆了好幾次，缺口掉出一個數字，然後門開了。

惰性求值

在 Haskell 裡，函式是天生懶惰的。每個函式，都只能接收一個參數。當我們定義了一個三參數的函式時，會是這樣的：

-- Haskell 語法
add :: Integer -> Integer -> Integer -> Integer
add x y z = x + y + z

而你可以把型別的部份看成是這樣：

add :: Integer -> (Integer -> (Integer -> Integer)))

換句話說，add 是一個接受一個 Integer，會回傳 (Integer -> (Integer -> Integer))) 型別的函式。

而如果我們繼續往下操作，會像是這樣的：

-- Haskell 語法
-- 在 Haskell 中，名稱後的空白就是 apply，不是其它語言常用的括號 ()

step1 = add 1
-- 此時 step1 就是回傳的那個 (Integer -> (Integer -> Integer))。
-- 把最外面的括號拿掉，就是 Integer -> (Integer -> Integer)

step2 = step1 2
-- 而重覆上面的步驟，step2 的型別是 Integer -> Integer，給一個整數，回傳一個整數的函式。

step2 3
-- 那麼再給一個數字就飽和囉。
-- => 6


-- 當然也可以一次給齊
add 1 2 3
-- => 6

Haskell 的函式，只要在不飽和的狀態，也就是未應用或被部份應用 (partially applied) 時，可以到處傳遞與組合。

組合

在 Elixir 裡，我們曾經用 |> 來表示將函式執行的結果，傳遞給下一個函式。像是這樣：

# Elixir 語法
result = 1 |> add_one() |> times_two() |> minus_three()

# add_one, times_two, minus_three 的定義

而這個可以在大多數語言裡，寫成被罵版 *的格式：

# Elixir 語法
result = minus_three(times_two(add_one(1)))

* 註：這個格式基本上只有在 LISP 系的方言裡受到擁戴。

而在數學上，這叫做函數的組合。我們可以把這個用數學的方式表示：

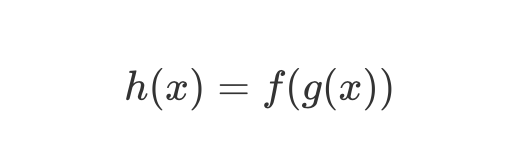
那麼既然函數是一等公民，我們可不可以不要管那個參數 x，而直接表達 h 函數，是 f 函數與 g 函數的組合呢？

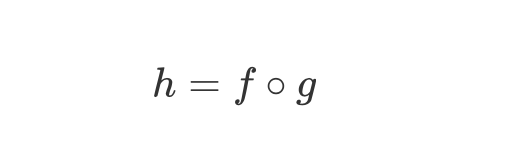
讓我們把這個翻譯回 Haskell，那麼 h 就是一個呼叫了之後，會先把參數傳給 g，再將其結果傳給 f 的函式：

-- Haskell 語法
h = f . g

要注意的是，這個跟 Elixir 的 |> 方向相反。 . 函式組合是由後往前傳的。

函式組合的型別規則

那麼讓我們把型別也放進函式的組合裡來看。當我們只有下面三個函式的型別定義，函式的內容本身還沒實作：

-- Haskell 語法
f :: Integer -> String
g :: Integer -> Integer
h :: String -> Integer

f = undefined
g = undefined
h = undefined

那麼就算我們還沒實作這三個函式，我們也可以知道以下幾個寫法是否正確：

-- Haskell 語法
i = f . g -- 可以。g 回傳 Integer, f 接收 Integer

j = g . f -- 不行。f 回傳 String, g 接收 Integer

k = h . g -- 不行。g 回傳 Integer, h 接收 String

l = f . h -- 可以，h 回傳 Integer, f 接收 Integer

m = h . f -- 可以，f 回傳 String, h 接收 String

n = h . f . g -- 可以

o = h . g . f -- 不行, 剛剛 j 那行 g.f 就失敗了

p = h . f . g . g . g . g . g . h . f . g -- 可以！ 

Haskell 的編譯器也知道。所以我們可以在定義完型別之後，還不需要實作函式就進行編譯，Haskell 就有辦法推導出接下來的組合是不是數學上合理的。如果不行，編譯就會失敗，如果可以那麼編譯會成功，只是如果執行會出錯而已。

curry 的真正優勢

當理解了函數式程式設計裡，最重要的函式可以組合這個本質後，就比較能夠意識到 curry 這種惰性求值手法的優秀之處。舉例來說，有個函式，需要三個參數才會飽和。而我們已經拿到其中兩個參數，最後一個參數，需經由複雜昂貴的計算，或是透過其它非同步的手段(如 AJAX) 才能拿到結果，那麼我們就可以這樣使用這個函式：

-- Haskell 語法
calc a b c = a + b + c

expensively_get_c url = undefined -- 一些很貴的計算

lazy_calc = calc 1 2 --先把已知的兩個參數套用，做成只差最後一個參數的 curry 函式
compose_calc = lazy_calc . expensively_get_c -- 接著把兩個函式組合在一起
result = compose_calc "https://random.num" -- 輸入昂貴計算所需的參數，調用整個函式

-- 當然也可以把第三行跟第四行改成一步做成組合函式：

compose_calc = (calc 1 2) . expensively_get_c
result = compose_calc "https://random.num" -- 呼叫的方式是一樣的

這個手法，在其它語言中也可以使用。例如 Elixir 的 |>，或 Ramda.js 的 R.compose 或 R.pipe，都能讓你較容易的運用函式組合的優秀之處。

組合自身

雖然 . 看起來像是個神奇的語法，但是其實它也只是一個函式而己。這是接收兩個函式，回傳一個函式的函式。型別是這樣：

-- Haskell 語法
(.) :: (b -> c) -> (a -> b) -> a -> c

可以更清楚的看到，接收的第一個函式型別 (b -> c) 的參數型別 b，必須要跟第二個函式型別 (a -> b) 的回傳型別 b 相同。而回傳的函式型別，就是第二個函式的接收型別 a，到第一個函式的回傳型別 c 的函式： a -> c。

函式與實值

而在最後，讓我們再把宣告變數，與定義函式這兩個的型別及語法並列一下：

-- Haskell
one :: Int
one = 1

add_one :: Int -> Int
add_one = (+ 1)

-- 示範呼叫
add_one 1 -- => 2

我們可以看出來，所謂函式，也不過只是實值的一種，差別在於這種實值可以呼叫與組合。或者，反過來說，所謂的實值，也不過就是需要零個參數的函式而己。

走過長廊，盡頭昏暗房間的中央，有個平台，上面鑲嵌了一張金屬的板子。上面寫著這樣的字，是程式碼吧…

calc_and_print :: Integer -> ???
calc_and_print = ???

calc_and_print 1 == "6"

桌面旁邊散落了很多文字的方塊。我看到 (+ 1)，show，(/ 2)，Integer，String，(* 10)，(* 3)，還有好幾個 .。

我想了想，選了六個方塊放上去。

整棟建築亮了起來。

[to be continue]