昨天，我們在實作的過程中，留下一個問題，就鑽石分級的定義，理論上，顏色D的價格 > 顏色E的價格 > 顏色F的價格。但是，「線性迴歸分析中」，顏色D的價格 跟 顏色F的價格很接近，但是，顏色E的價格，卻偏低......
　　今天我們就來找找原因：
　　1. 先看看昨天的公式
　　顏色D : price = 8510carat - 2478; 1克拉 = 6032; 2克拉 = 14,542; 3克拉 = 23,052
　　顏色E : price = 7962carat - 2257; 1克拉 = 5705; 2克拉 = 13,667; 3克拉 = 21,629
　　顏色F : price = 8678carat - 2434; 1克拉 = 6244; 2克拉 = 14,992; 3克拉 = 23,67０

　　2. 我們在Tableau中，建一個平均值的表格。我先把克拉換成整數，從數字觀察上，我們預期，Color=E, Carat=1, 這個地方的平均應該在 7800附近。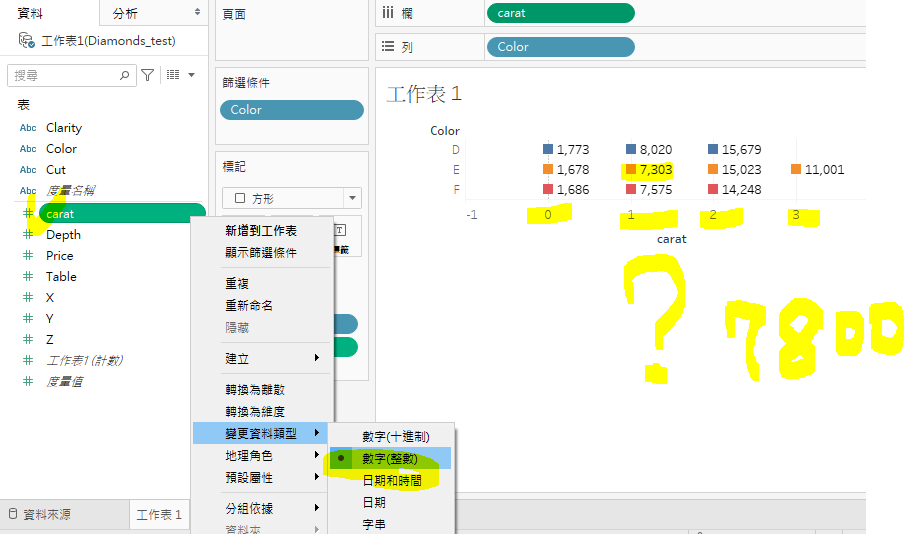

　　3. 來寫一個小公式吧！把統計區間縮小。
　　
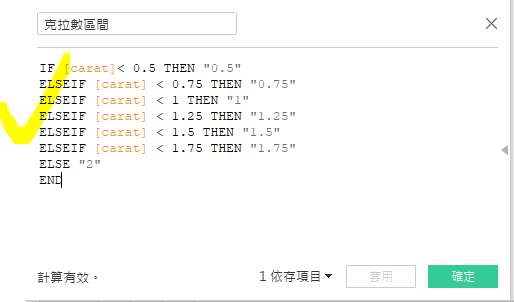
　　4. 先來看看平均價格。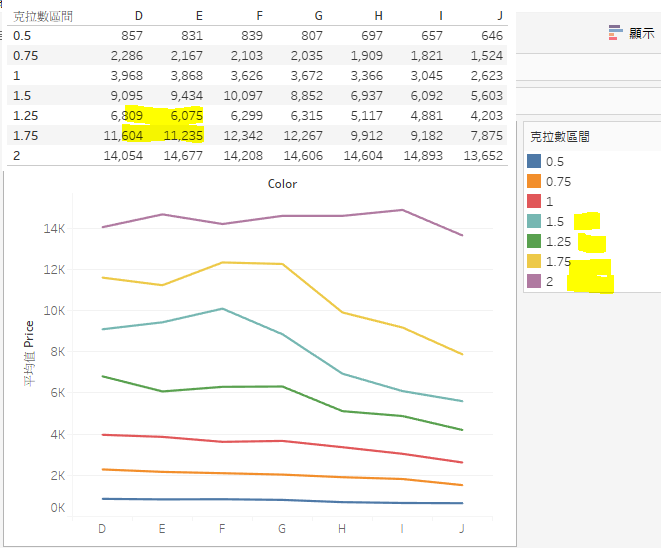

　　5. 再來看看樣本數量。由這兩個圖表來看，在1克拉以下的數據，與假設的較符合，但是，1克拉以上就不符合，因此，只能再進一步研究這個部分的數據。另外，1,25克拉以上的數據偏少，價格平均值容易受到極端值影響。
　　
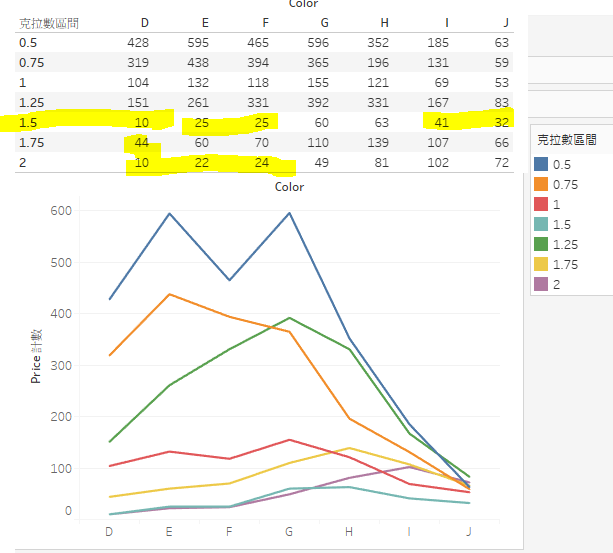
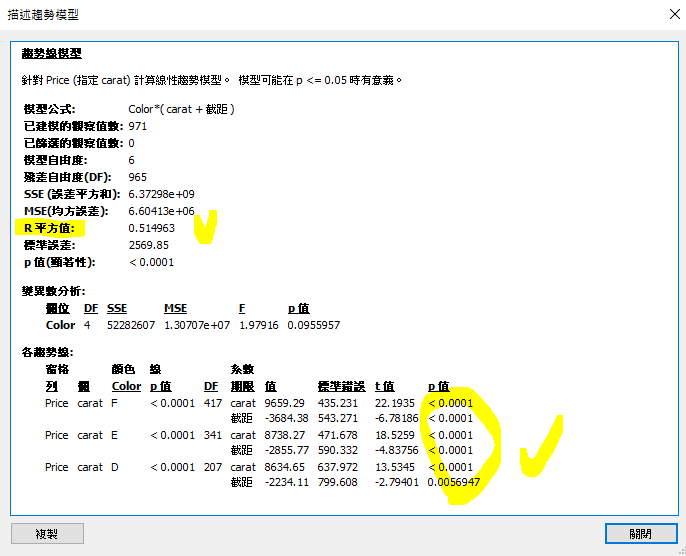
　　6. 將資料範圍限定，重畫昨天的圖(carat > 1)。雖然Ｐ值很低(無法拒絕)，但R平方在51附近，資料解釋能力並不高。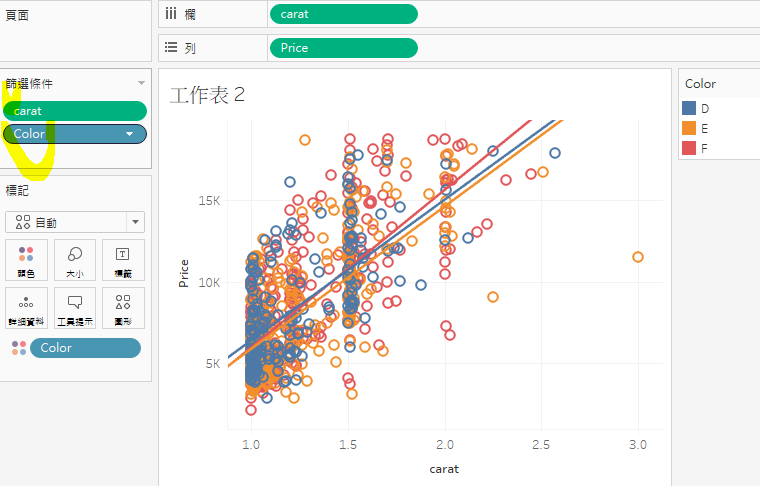


　　7. 把4C合在一起。這張圖，隱約可以看出資料量對回歸分析的影響。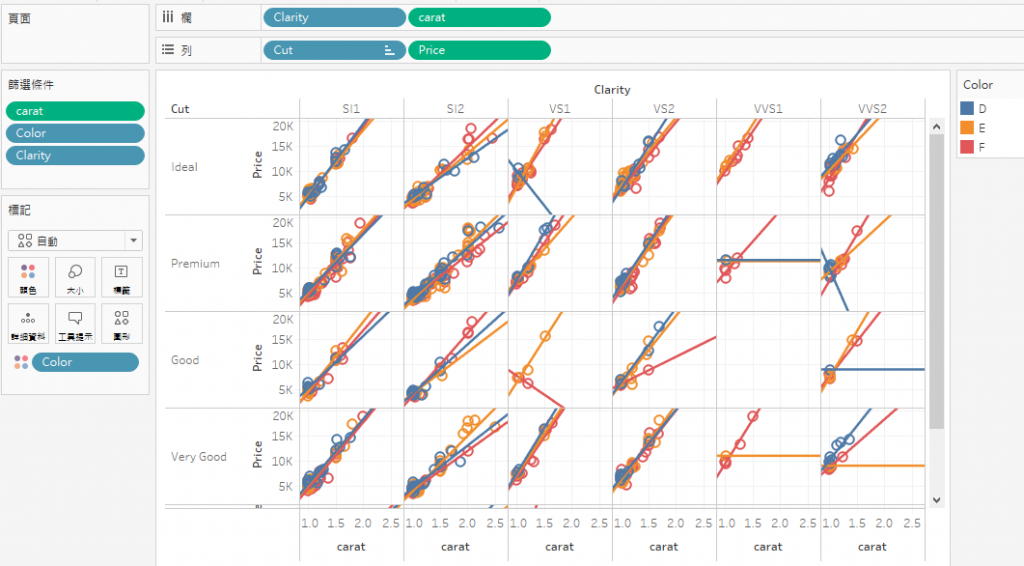

　　我想，鑽石的價格策略，都是依照 4C標準去制定的。這也是為什麼在1克拉以下，加上數據量大的時候，迴歸分析結果，跟我們假設(預期)的很接近。但是，如果數據量不大(如下圖)，1.4克拉以下，整個價格邏輯還是follow 4C的市場共識，但是，1.6克拉以上，有三顆 2克拉附近的鑽石，被高價賣出，讓整個線圖走揚。
　　

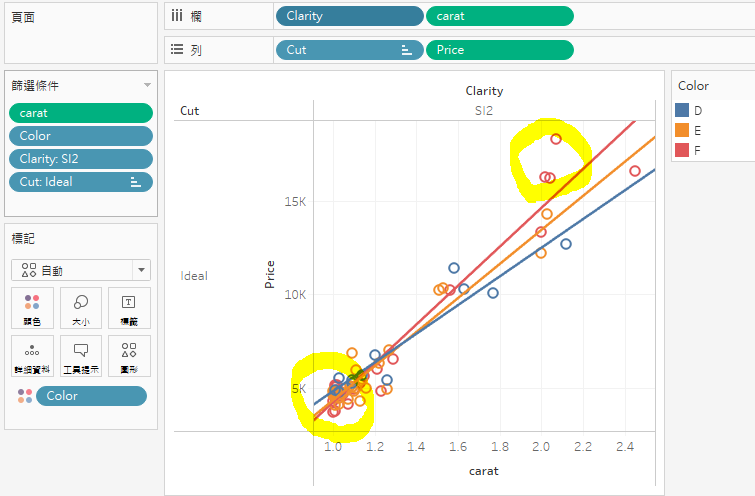
　　看來，「大數據分析」就是要努力去尋找「看似沒有關係，事實上，可能存在某種關係。」這一類充滿挑戰性的虛擬問題啊！