形式神經元變形

(原文網址：https://kknews.cc/tech/z34j3rg.html)

• 目前常用的神經元形式，是上述模型的一個簡單變形，把閾值（threshold）變成偏置（b,bias）就可以得到。

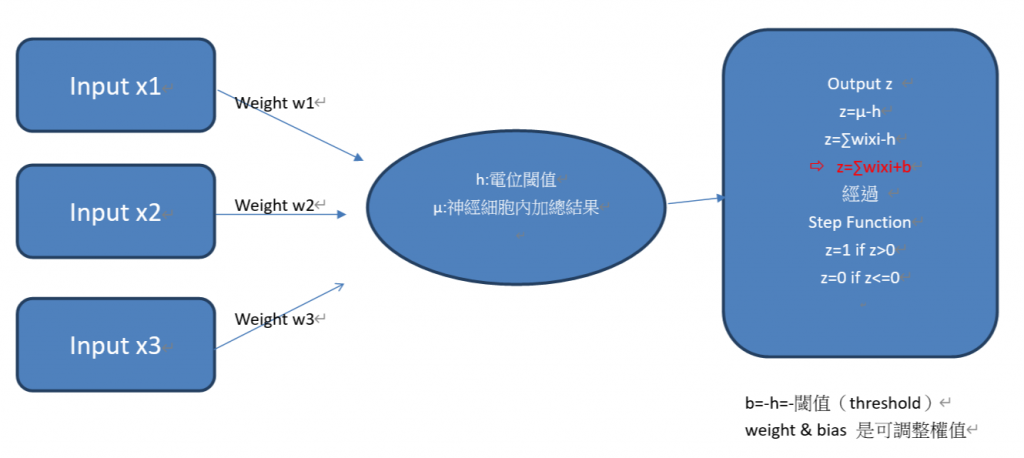
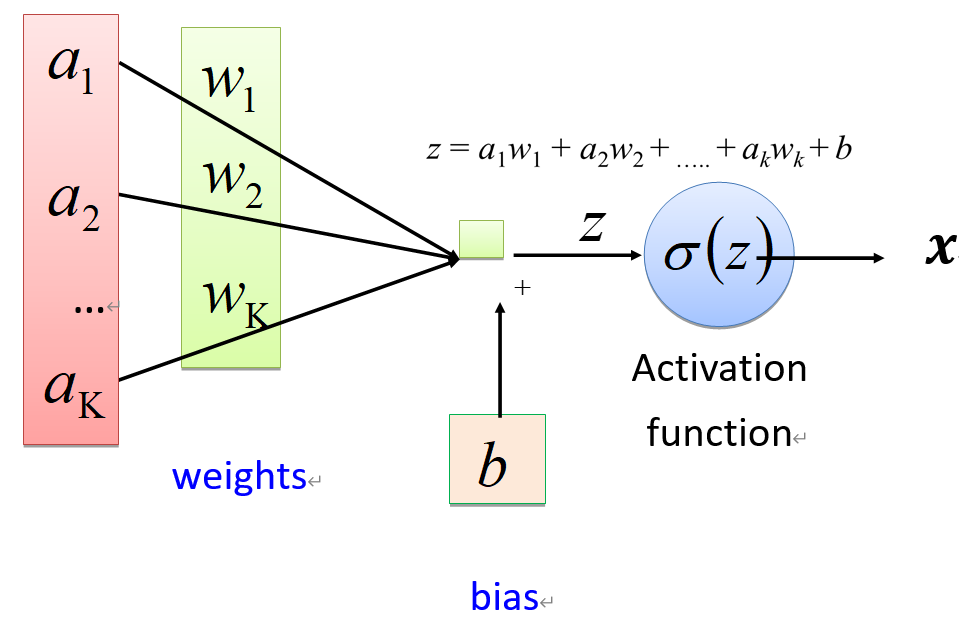
形式神經元加上感知器(Perceptron)

(原文網址：https://kknews.cc/tech/z34j3rg.html )

• 單層神經網絡 :首個可以學習的神經網絡
  • 1958年，Rosenblatt提出了一種由兩層神經元組成的神經網絡--感知機模型（Perceptron），它是首個可以學習的神經網絡
  • 與神經元模型重大區別在於感知機的參數並不是事先設定的而是訓練得到的，具體做法是通過在MCP模型的基礎上使用損失函數（loss function），通過降低損失函數值就可以更新參數。學習參數的過程在幾何上是在學習「決策分界」。即在二維的數據平面中學得一條直線，3維的數據平面中學得一個平面，n維的數據平面中學得n-1維的超平面。
  • 1962年，單層感知機模型的收斂性得到理論證明。
• 多層感知機（MLP）:非線性分類
  • Minsky指出單層神經網絡無法解決異或問題。雖然，通過增加中間的計算層多層神經網絡就可以解決異或問題，而且還具有非常好的非線性分類效果。不過Minsky認為如果將計算層增加到多層會導致計算量過大，也沒有有效的學習算法，所以研究更深層的網絡是沒有價值的。
  • 1986年，神經網絡研究迎來了轉機，Rumelhar和Hinton等人提出了著名的反向傳播（Backpropagation，BP）算法，解決了多層神經網絡產生的複雜計算量問題，人工神經網絡的研究迎來復甦。
    從此開啟”多層感知機（MLP） “

多層感知機（MLP）

(原文網址：https://kknews.cc/tech/z34j3rg.html)

• 普通的多層神經網絡也叫做多層感知機（MLP），它是在輸入層，輸出層的基礎上又增加了做計算的隱藏層（在輸入層與輸出層之間所以稱作「隱藏」層）。理論證明，多層神經網絡可以無限逼近任意連續函數，也就是說，面對複雜的非線性分類任務也可以分類的很好。
• 結構如下：

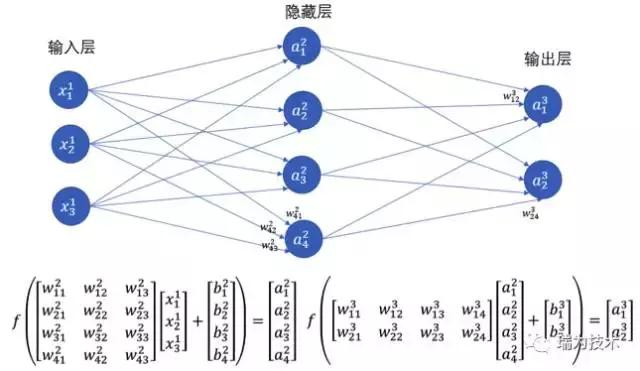
註:本文是搜尋數個網站及各種不同來源之結果,著重在學習,有些內容已難辦別出處,我會儘可能列入出處,若有疏忽或出處不可考,請聯絡我, 我會列入, 尚請見諒。