只有距離。
有 distance 距離與 direction 方向。
超過三維以上則稱 tensor 張量
以下會主要以向量為主討論。
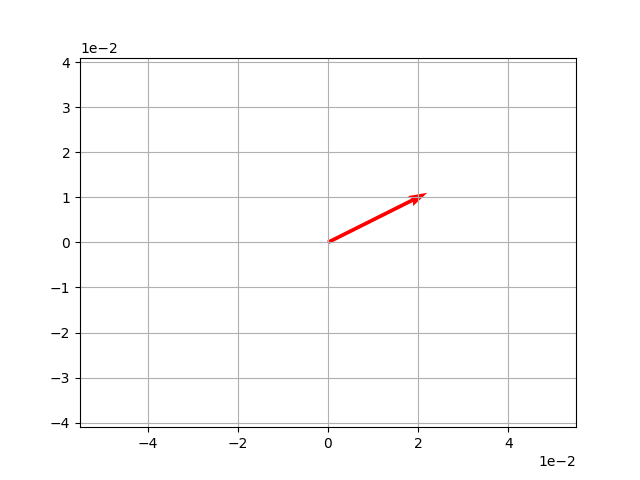
import numpy as np
import matplotlib.pyplot as plt
# We'll use a numpy array for our vector
v = np.array([2,1])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, *v, scale=10, color='r') # quiver畫箭頭,*表示展開
plt.show()
import numpy as np
vMag = np.linalg.norm(v)
print (vMag)
>> 2.23606797749979
例子:tan(a) = 1/2,則 a = tan−1(0.5) ≈ 26.57
import math
import numpy as np
# 向量座標
v = np.array([2,1])
vTan = v[1] / v[0]
print ('tan = ' + str(vTan))
>> tan = 0.5
# 三角函數轉換
vAtan = math.atan(vTan)
print('radian =', vAtan) # 逕度
>> radian= 0.4636476090008061
# 或 math.degrees(vAtan)
print('degree =', vAtan*(360/(2*math.pi))) # 角度
>> degree = 26.56505117707799
# 1-4. Vector add
import math
import numpy as np
import matplotlib.pyplot as plt
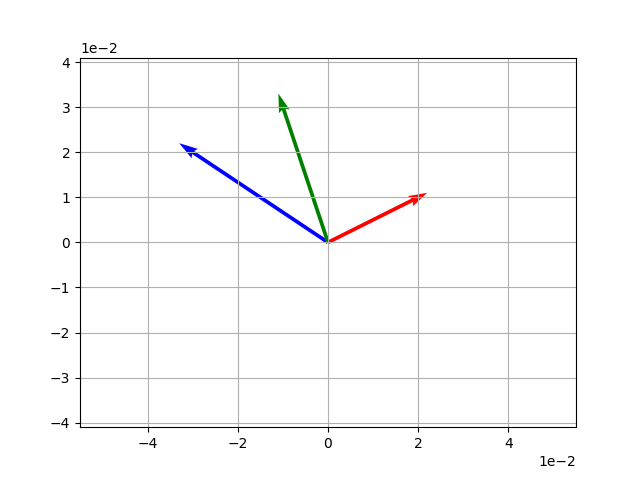
v = np.array([2, 1]) # 力 1
s = np.array([-3, 2]) # 力 2
z = v + s # 合力
# Plot v and s
vecs = np.array([v, s, z])
origin = [0, 0, 0], [0, 0, 0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:, 0], vecs[:, 1], color=['r', 'b', 'g'], scale=10)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import math
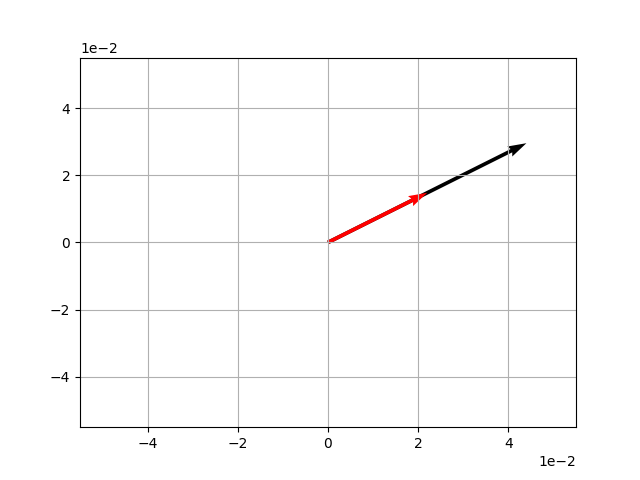
v = np.array([2,1])
w = 2*v
# 作圖
vecs = np.array([w, v])
origin = [0, 0], [0, 0]
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:, 0], vecs[:, 1], color = ['k', 'r'], scale=10)
plt.show()
vs = (v1s1) + (v2s2) + ... + (vnsn)
數學意義為 v 在 s 上的投影,物理意義為對特定方向"作功"。
數學證明如下: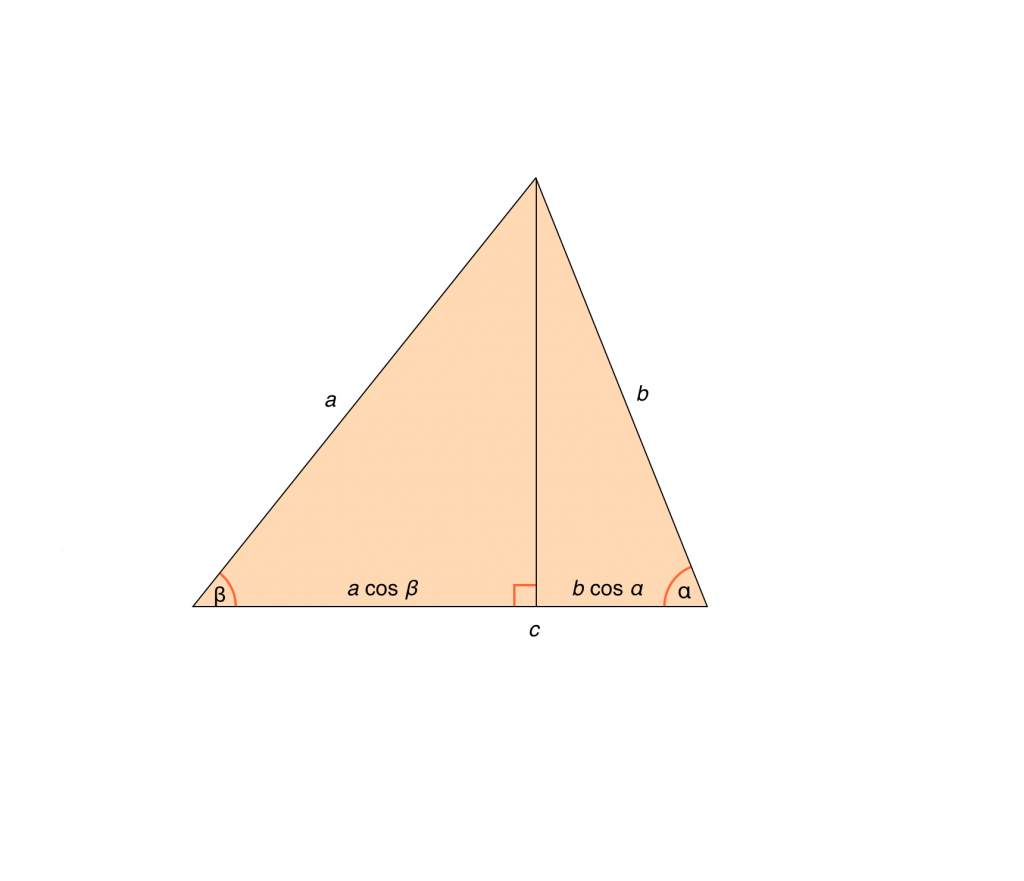

import numpy as np
v = np.array([2, 1])
s = np.array([-3, 2])
d = v @ s
# 或 d = v.dot(s)
print(d)
>> -4
當然,換個說法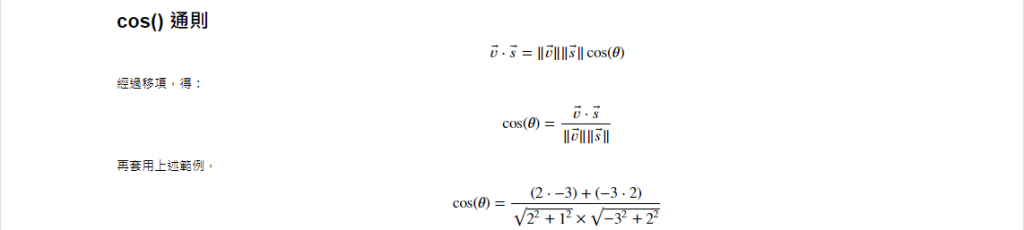
以下是 python 的實際程式碼:
import math
vMag = np.linalg.norm(v)
sMag = np.linalg.norm(s)
cos = v @ s / (vMag * sMag)
theta = math.degrees(np.arccos(cos))
print(theta)
>> 119.74488129694222
import numpy as np
X = np.arange(1,7).reshape(2,-1) # -1 會自動計算合理的分配數
print(X)
>> [[1 2 3]
[4 5 6]]
首先,我們建立三個矩陣:
import numpy as np
A = np.array([[1,2,3],
[4,5,6]])
B = np.array([[6,5,4],
[3,2,1]])
C = np.array([[9,8],
[7,6],
[5,4]])
print(A + B)
>> [[7 7 7]
[7 7 7]]
print(A - B)
>> [[-5 -3 -1]
[ 1 3 5]]
C1. Scalar Multiplication
print(2 * A)
>> [[ 2 4 6]
[ 8 10 12]]
C2. Dot
print(A @ C) # 矩陣 2*3 x 矩陣 3*2 → 矩陣 2*2
>> [[ 38 32]
[101 86]]
print(C @ A) # 矩陣 3*2 x 矩陣 2*3 → 矩陣 3*3
>> [[41 58 75]
[31 44 57]
[21 30 39]]
不論任何矩陣乘以單位矩陣,都將等於自身矩陣。
import numpy as np
A = np.array([[1,2,3],
[4,5,6],
[7,8,9]])
one = np.eye(3)
print(one)
>> [[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
print(A @ one)
>> [[1. 2. 3.]
[4. 5. 6.]
[7. 8. 9.]]
任何矩陣乘以自身反矩陣會等於單位矩陣。
A.A^-1 = I
import numpy as np
a = np.array([[1, 2],
[3, 4]
])
print(np.linalg.inv(a))
>> [[-2. 1. ]
[ 1.5 -0.5]]
x + y = 16
10x + 25y = 250
提示:A.X = B,則 X = A^−1.B
A = np.array([
[1, 1],
[10, 25]])
B = np.array([16, 250])
print(np.linalg.inv(A) @ B)
# 其結果會等同 np.linalg.solve(A, B)
>> [10. 6.]
常在特徵轉換(降維)的過程中用到,以下分開解釋。
import numpy as np
import matplotlib.pyplot as plt
v = np.array([1, 0])
A = np.array([[2,1],
[1,2]])
t = A @ v
original = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0, 0))
plt.quiver(*origin, *t, color='orange', scale=10)
plt.quiver(*origin, *v, color='blue', scale=10)
plt.show()
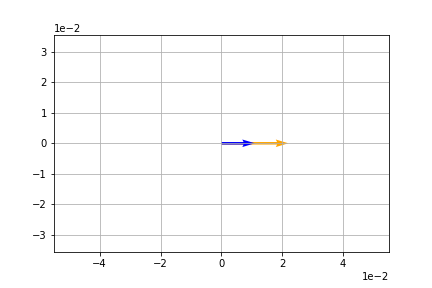
import numpy as np
import matplotlib.pyplot as plt
v = np.array([1,0])
A = np.array([[0,-1],
[1,0]])
t = A@v
print (t)
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, *t, color='orange', scale=10)
plt.quiver(*origin, *v, color='blue', scale=10)
plt.show()
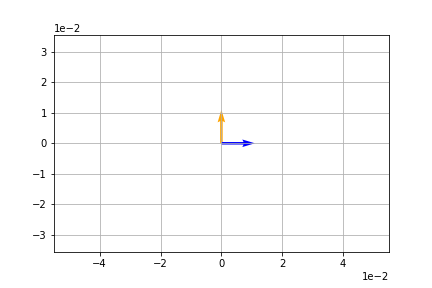
import numpy as np
import matplotlib.pyplot as plt
v = np.array([1,0])
A = np.array([[2,1],
[1,2]])
t = A@v
print (t)
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, *t, color='orange', scale=10)
plt.quiver(*origin, *v, color='blue', scale=10)
plt.show()
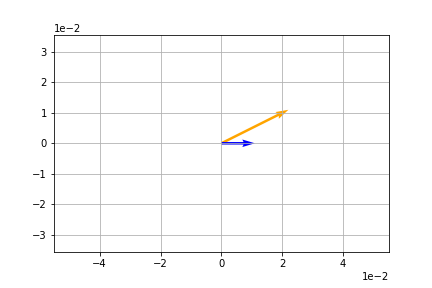
當變換僅"影響尺度"時"變換矩陣"與"常數"等效:
v = np.array([1,0])
A = np.array([[2,0],
[0,2]])
t1 = A@v
t2 = 2*v
print(t1, t2)
>> [2 0] [2 0]

當然,numpy 很貼心的提供了 Eigenvectors and Eigenvalues 的算法:
import numpy as np
A = np.array([[2, 0],
[0, 3]])
eVals, eVecs = np.linalg.eig(A)
print('Eigenvalue:\n', eVals)
print('Eigenvector:\n', eVecs)
>> Eigenvalue:
[2. 3.]
Eigenvector:
[[1. 0.]
[0. 1.]]
.
.
.
.
.
import numpy as np
import matplotlib.pyplot as plt
from sympy.core.symbol import Symbol
# 梯度下降法
def GD(x_start, df, epochs, lr):
xs = np.zeros(epochs+1)
x = x_start
xs[0] = x
for i in range(epochs):
dx = df(x)
x += -dx * lr
xs[i+1] = x
return xs
f(x) = x^3 - 2x + 100
超參數:
x_start = 2
epochs = 1000
learning_rate = 0.01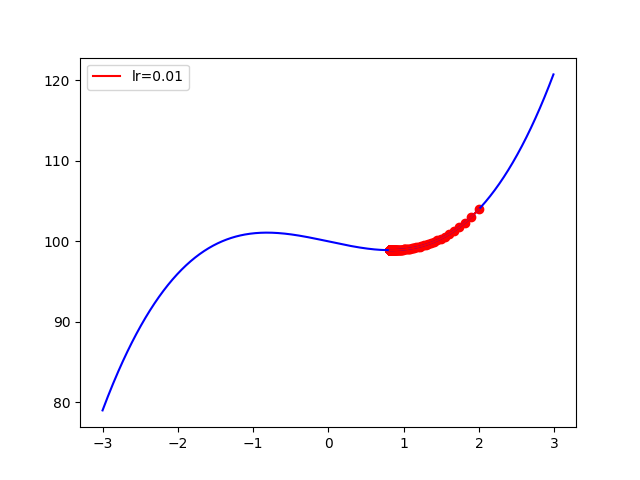
f(x) = -5x^2 + 3x + 6
x_start = 2
epochs = 1000
learning_rate = 0.01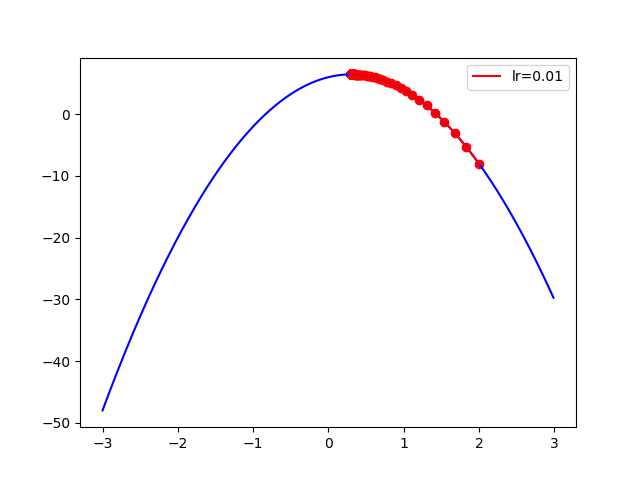
f(x) = 2x^4 - 3x^2 + 2x - 20
x_start = 5
epochs = 1000
learning_rate = 0.001 # 必須要設定小,否則會左右橫跳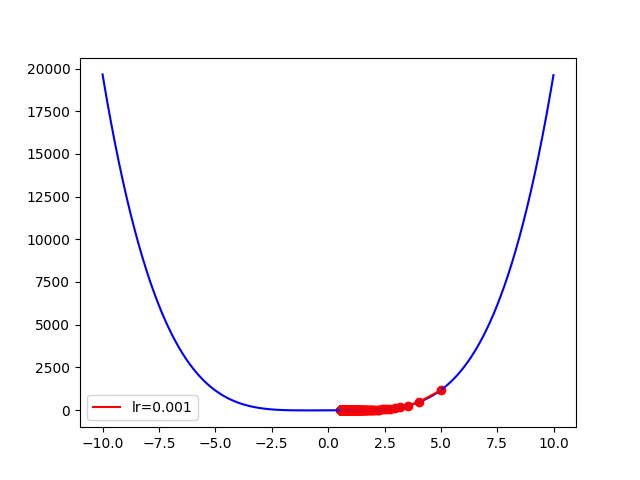
f(x) = sin(x)e^(-0.1(x-0.6)^2)
此時要注意先把函數的一階導函數求出來,我們運用 sympy 達成。
from sympy import *
x = Symbol('x')
y = sin(x)* E ** (-0.1*(x-0.6)**2)
dy = y.diff(x) # 把方程式微分求一階導函數
def func(x):
return np.sin(x)*np.exp(-0.1*(x-0.6)**2)
def dfunc(x_self):
return dy.subs(x, x_self).evalf() # 把 x_self 用 sub 函數迭代入 dy
接著就可以畫出梯度下降啦,要注意的僅剩下起始點的取值了
4-1.
x_start = 0.3
epochs = 1000
learning_rate = 0.01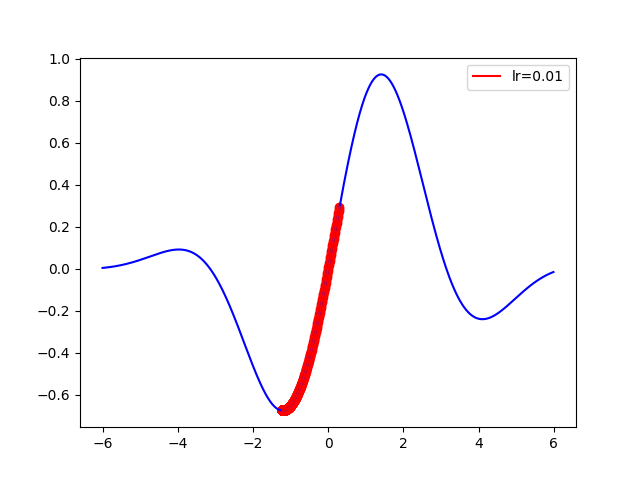
4-2.
x_start = 2.5
epochs = 1000
learning_rate = 0.01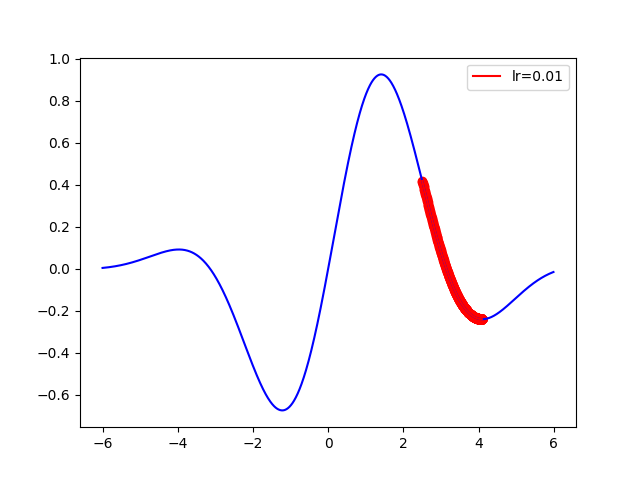
.
.
.
.
.
https://ithelp.ithome.com.tw/articles/10222877?sc=rss.iron
max z = 4x + y
3x + 2y <= 6
6x + 2y <= 10
x, y >=0
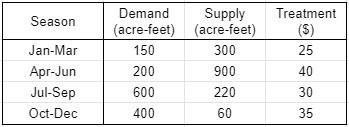
對話機器人分析對話,通常會將其轉為矩陣,進行比對才輸出。
#語料
corpus = [
'This is the first document.',
'This is the second second document.',
'And the third one.',
'Is this the first document?',
]
from sklearn.feature_extraction.text import CountVectorizer
#將文件中的詞語轉換為詞頻矩陣
vectorizer = CountVectorizer()
#計算個詞語出現的次數
X = vectorizer.fit_transform(corpus)
#獲取詞袋中所有文件關鍵字
word = vectorizer.get_feature_names()
print ("word vocabulary=", word)
>> word vocabulary= ['and', 'document', 'first', 'is', 'one', 'second', 'the', 'third', 'this']
print ("BOW=", X.toarray())
>> BOW= [[0 1 1 1 0 0 1 0 1]
[0 1 0 1 0 2 1 0 1] # 第六個詞 "second" 出現 "2" 次
[1 0 0 0 1 0 1 1 0]
[0 1 1 1 0 0 1 0 1]]
from sklearn.feature_extraction.text import TfidfTransformer
transformer = TfidfTransformer()
print ("transformer=", transformer)
>> transformer= TfidfTransformer()
# TF-IDF值
tfidf = transformer.fit_transform(X)
# 查看資料結構 tfidf[i][j] 表示 i 類文件中的 tf-idf 權重
print ("tfidf=", tfidf.toarray())
>> tfidf= [[0. 0.43877674 0.54197657 0.43877674 0. 0.
0.35872874 0. 0.43877674]
[0. 0.27230147 0. 0.27230147 0. 0.85322574
0.22262429 0. 0.27230147]
[0.55280532 0. 0. 0. 0.55280532 0.
0.28847675 0.55280532 0. ]
[0. 0.43877674 0.54197657 0.43877674 0. 0.
0.35872874 0. 0.43877674]]
from sklearn.metrics.pairwise import cosine_similarity
print (cosine_similarity(tfidf[-1], tfidf[0:-1], dense_output=False))
>> (0, 2) 0.1034849000930086
(0, 1) 0.43830038447620107
(0, 0) 1.0 # 100% 相似 (cos = 1)
