Chap.I 理論基礎

Part 4：統計 & 機率

Analyze the data through data visualization using Seaborn

圖片出處

1. Data and Data Visualization

1-1. Introduction to Data

統計是基於資料所推演出來的資訊，包括一些描述、數量及衡量。
資料集(dataset)：又稱樣本。包括 Observations 觀察值或 Cases 案例，即資料集的列。
attributes 屬性或 features 特徵：資料集或觀察值的欄位。

import statsmodels.api as sm

# 取出內建資料集 (父母對小孩身高)
# https://www.statsmodels.org/devel/datasets/index.html

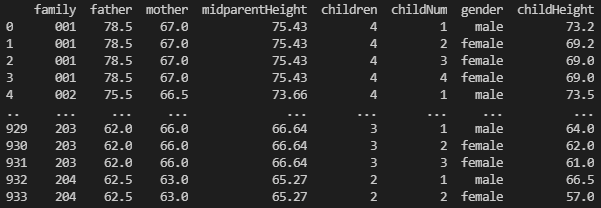
df = sm.datasets.get_rdataset('GaltonFamilies', package='HistData', cache=True).data
print(df)

1-2. Qualitative Data：定性資料，類別欄位

a. Nominal Data: 欄位值並沒有大小的隱含意義。
one-hot encoding: 欄位顏色(紅/藍/綠)，會將其拆成: 欄位紅(是/否)、欄位藍(是/否)、欄位綠(是/否)
b. Ordinal Data: 欄位值有大小的隱含意義。
Discrete Data: 離散資料，通常會用分類演算法。
Continuous Data: 連續資料，通常會用迴歸演算法。
少部分如: 目標年齡層客群 (15~20歲)，會將資料做成離散資料演算法。q

補充：Interval vs. Ratio
Interval：數值可比較，但無零的概念。例如溫度 0度，又 20 度並不是 10 度的兩倍。
Ratio：數值可比較，也有零的概念。例如身高、體重及時間長度。

補充：Sample vs Population
樣本(Sample) 與 母體(Population)
台北市長選舉：全體市民>=20歲 ==> 母體(Population)
抽樣調查1000份 ==> 樣本(Sample)

1-3. Visaulization

我們先取用一個 Datasets

import statsmodels.api as sm

df = sm.datasets.get_rdataset('GaltonFamilies', package='HistData', cache=True).data

A. 長條圖 Bar chart

多用於比較資料不同樣本差異。
A1. matplotlib

import matplotlib.pyplot as plt
import matplotlib.font_manager as fm

genderCounts.plot(kind='bar', title='Gender Counts')

# 中文化: 指定中文字體
zhfont1 = fm.FontProperties(fname='C:\Windows\Fonts\kaiu.ttf', size=20)
plt.xlabel('性別 (Gender)',fontproperties=zhfont1)
plt.xticks(rotation=30)
plt.ylabel('Number of Children')

plt.show()

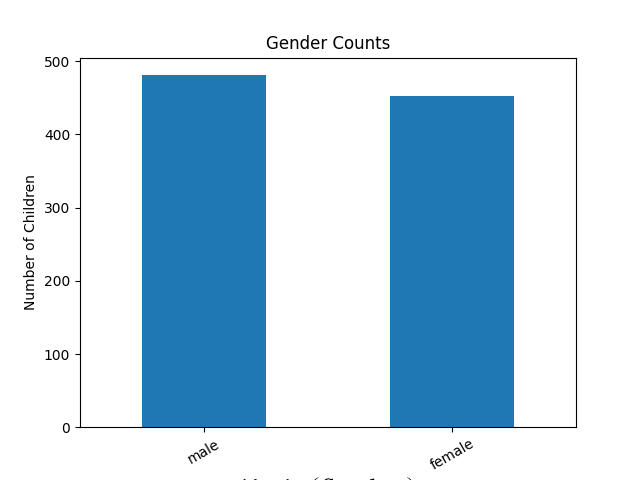
A2. seaborn (基礎架構在 mayplotlib 上)

import matplotlib.pyplot as plt
import seaborn as sns

# 性別 vs. 小孩身高
sns.barplot(x='gender', y='childHeight', data=df)
plt.show()

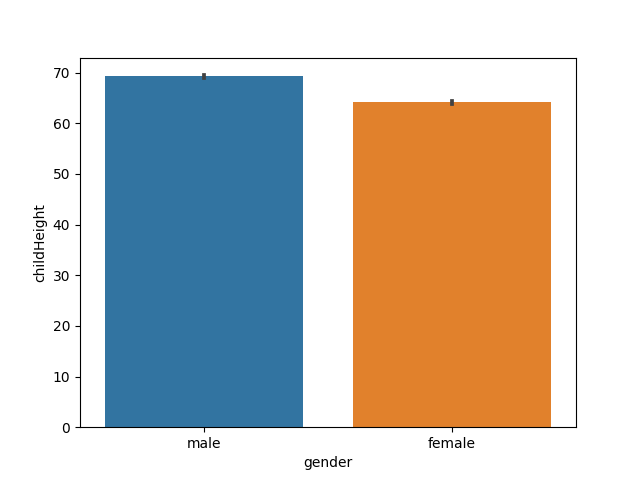
# 家中小孩數 vs. 小孩身高
sns.barplot(x='children', y='childHeight', data=df)
plt.show()

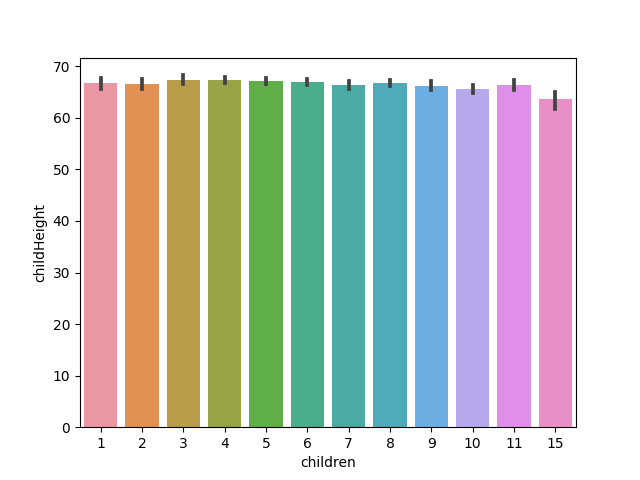
# 用 hue= ，家中小孩數&小孩排名 vs. 小孩身高
sns.barplot(x='children', y='childHeight', hue='childNum', data=df)
plt.legend('')
plt.show()

B. 直方圖 Histogram

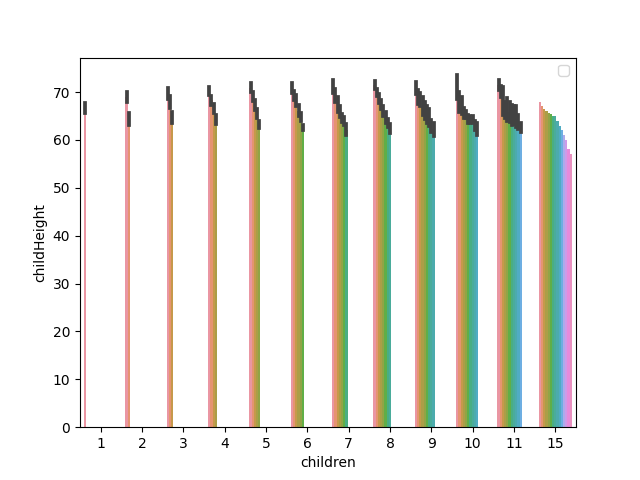
多用於觀察資料分布、是否有極端值...等。

import seaborn as sns
import matplotlib.pyplot as plt

sns.distplot(df['father'], bins=10, kde=True)
plt.show()

C. 圓餅圖 Pie plot

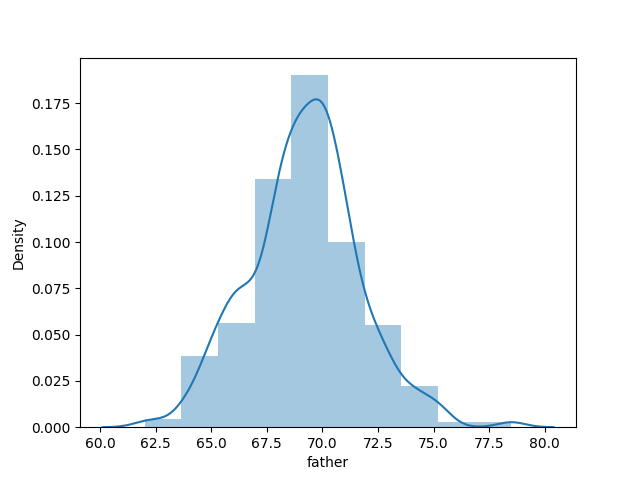
用於觀察資料樣本簡單分布。
PS. secborn 並沒有 pie plot 畫法

import seaborn as sns
import matplotlib.pyplot as plt

genderCounts.plot(kind='pie', title='Gender Counts', figsize=(6,6)) #,explode=[0.2, 0.])
plt.show()

D. 散布圖 Scatter plots

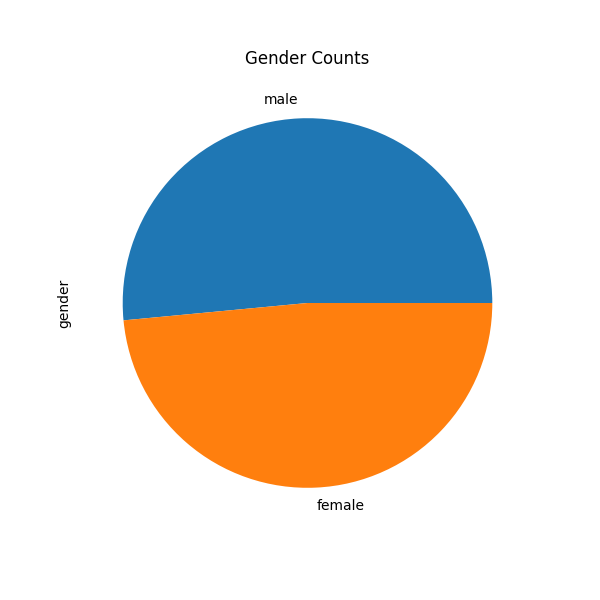
觀察定量特徵間的關係，也可以觀察是否有離群值 (outliers)

import seaborn as sns
import matplotlib.pyplot as plt

Heights = df[['midparentHeight', 'childHeight']]

Heights.plot(kind='scatter', title='Parent vs Child Heights', x='midparentHeight', y='childHeight')
plt.xlabel('Avg Parent Height')
plt.ylabel('Child Height')

plt.show()

E. 線性圖 Line chart

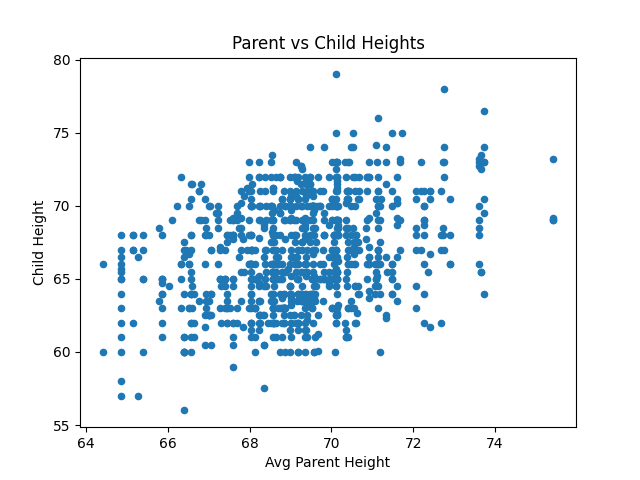
import seaborn as sns
import matplotlib.pyplot as plt

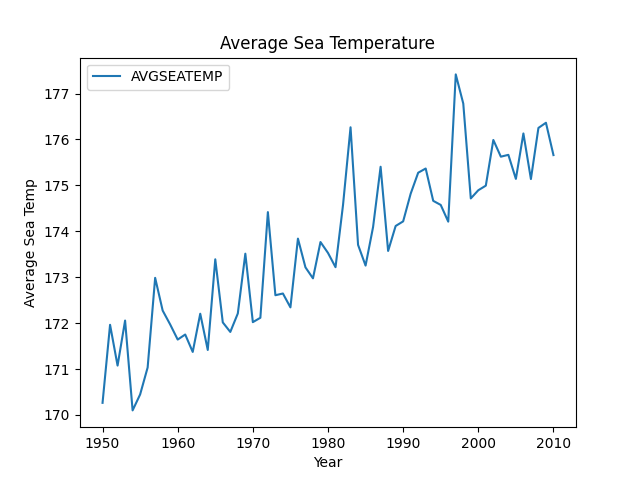
df = sm.datasets.elnino.load_pandas().data
print(df)

df['AVGSEATEMP'] = df.mean(1)
print(df['AVGSEATEMP'])

df.plot(title='Average Sea Temperature', x='YEAR', y='AVGSEATEMP')
plt.xlabel('Year')
plt.ylabel('Average Sea Temp')

plt.show()

.
.
.
.
.

Homework Ans：

1. 依據網頁內容，規劃人力資源

max z = 4x + y
3x + 2y <= 6
6x + 2y <= 10
x, y >=0

import pulp as p 

# 建立線性規劃 求取目標函數的最大值
Lp_prob = p.LpProblem('Problem', p.LpMaximize)

# 宣告變數(Variables)
x = p.LpVariable("x", lowBound = 0) # x 最小不能小於0
y = p.LpVariable("y", lowBound = 0) # y 最小不能小於0

# 定義目標函數(Objective Function)
Lp_prob += 4 * x + y

# 定義限制條件(Constraints)
Lp_prob += 3 * x + 2 * y <= 6
Lp_prob += 6 * x + 3 * y <= 10

# 求解
status = Lp_prob.solve()

# 顯示答案 
print(p.value(x), p.value(y), p.value(Lp_prob.objective))
>> 1.6666667 0.0 6.6666668

HW2. 供水需求、供給、處理費如下。若供水留給下季使用，每單位儲水成本增加$10，問全年最小成本為?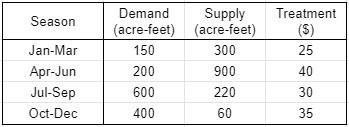

首先，令：
1. 成本(所求) = 當季存儲(未知) * 10 + 當季處理(未知) * 當季價格
2. 當季存儲(未知) <= 當季供給 + 上季存儲(未知) - 當季需求
3. 當季處理(未知) >= 當季需求 + 當季存儲(未知)

# 建立線性規劃 求取目標函數的最小值
Lp_prob = p.LpProblem('Problem', p.LpMinimize)

# 宣告變數(Variables)
# 儲水量
x1 = p.LpVariable("x1", lowBound = 0) # Create a variable x >= 0
x2 = p.LpVariable("x2", lowBound = 0) # Create a variable x >= 0
x3 = p.LpVariable("x3", lowBound = 0) # Create a variable x >= 0
x4 = p.LpVariable("x4", lowBound = 0) # Create a variable x >= 0

# 處理量
y1 = p.LpVariable("y1", lowBound = 0) # Create a variable y >= 0
y2 = p.LpVariable("y2", lowBound = 0) # Create a variable y >= 0
y3 = p.LpVariable("y3", lowBound = 0) # Create a variable y >= 0
y4 = p.LpVariable("y4", lowBound = 0) # Create a variable y >= 0

# 定義目標函數(Objective Function)
Lp_prob += (x1 + x2 + x3 + x4)*10 + y1*25 + y2*40 + y3*30 + y4*35

# 定義限制條件(Constraints)
Lp_prob += x1 <= 300 + 0 - 150
Lp_prob += x2 <= 900 + x1 -200
Lp_prob += x3 <= 220 + x2 - 600
Lp_prob += x4 <= 60 + x3 - 400

Lp_prob += y1 >= 150 + x1
Lp_prob += y2 >= 200 + x2
Lp_prob += y3 >= 600 + x3
Lp_prob += y4 >= 400 + x4

# 求解
status = Lp_prob.solve()

# 顯示答案
x = [x1, x2, x3, x4]
y = [y1, y2, y3, y4]
for i in range(4):
    print(p.value(x[i]), p.value(y[i]), p.value(Lp_prob.objective))

>> 20.0 170.0 94050.0
   720.0 920.0 94050.0
   340.0 940.0 94050.0
   0.0 400.0 94050.0