貪婪(Greedy)演算法

貪婪演算法是考慮局部最佳解，在子結構中解決問題是相當有利的，但放入整體問題中，不一定會是最佳解。

貪婪演算法與動態規劃的不同在於它對每個子問題的解決方案都做出選擇，不能回退。動態規劃則會儲存以前的運算結果，並根據以前的結果對當前進行選擇，有回退功能。
參考資料：wiki

戴克斯特拉演算法(Dijkstra's algorithm)

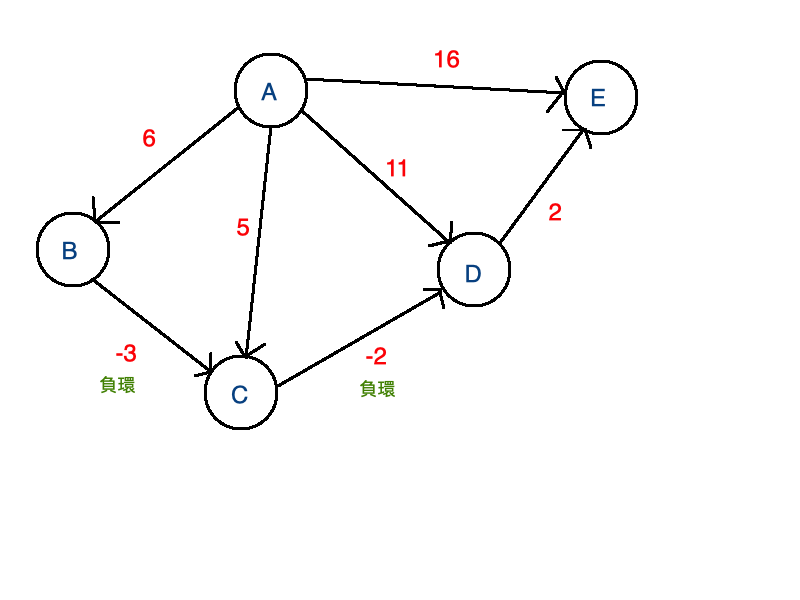
Dijkstra's algorithm與Bellman-Ford Algorithm一樣，能夠正確求出有向圖的最短路徑。但圖形中若有負值時，Dijkstra's Algorithm無法求出正確路徑。迴圈中有負環時，並不存在最短路徑。Bellman-Ford Algorithm可以判斷出最短路徑不存在，但Dijkstra's Algorithm會將錯誤的判斷當作正確答案。因此，無法使用Dijkstra's Algorithm無法用於負環的圖形。
總結：若邊沒有負環，選擇執行時間的Dijkstra's Algorithm較佳。邊有負環時，則使用Bellman-Ford Algorithm，執行時間雖長，但可以正確求解。

影片參考：
https://www.youtube.com/watch?v=pVfj6mxhdMw

from heapq import *
City = {}
G = {}
pq = []
# dis為101個元素的串列，每個元素值都是1000000
dis = [1000000]*101
# v為101個元素的串列，每個元素值都是0
v = [0]*101
# 將節點名稱轉成數字，使用字串p為輸入參數，將節點名稱p轉換成節點編號
def getCityIndex(p):
    # 若p不是City的key，則設定City[p]
    if p not in City.keys():
        # 對應的值為City的長度
        City[p]=len(City)
    # 回傳City key的對應值
    return City[p]

class Edge:
    def __init__(self, s, t, w):
        # s：邊的起點，t：邊的終點，w：邊的權重
        self.s = s
        self.t = t
        self.w = w

n = int(input())
for i in range(m):
    # 每次輸入三個資料，表示邊的兩個頂點到變數a與b，邊的權重到變數w
    a, b, w = input().split()
    a = getCityIndex(a)
    b = getCityIndex(b)
    w = int(w)
    e1 = Edge(a, b, w)
    e2 = Edge(b, a, w)
    if a in G.keys():
        G[a].append(e1)
    else:
        G[a]=[e1]
    if b in G.keys():
        G[b].append(e2)
    else:
        G[b]=[e2]

# 輸入起點節點名稱，傳入getCityIndex轉換成節點編號，變數s參考到此節點編號
s = getCityIndex(input())
# 建立有兩個元素的tuple，目標點起始點為s
p = (0, s) #(距離,目標點)
heappush(pq, p)
# 表示出發點的最短距離為0
dis[s]=0

while len(pq) > 0:
    # 使用heappop取出最上面元素（起始點到此點是最短距離）
    p = heappop(pq)
    # s為p的第二個元素，為該邊的目標點起點，是下一個起點
    s = p[1]
    # 若v[s]=0，設定v[s] = 1，表示起始點到節點編號s是最短路徑
    if v[s] == 0:
        v[s] = 1
        for edge in G[s]:
            if v[edge.t] == 0:
                if dis[edge.t] > dis[s] + edge.w:
                    dis[edge.t] = dis[s] + edge.w
                    p = (dis[edge.t], edge.t) #(距離,目標點)
                    heappush(pq, p)

for i in range(len(City)):
    print(dis[i]," ", sep="",end="")
print()

程式碼參考資料：資料結構使用Python

負環

負環就是最短路徑所形成的循環，若不斷經過此循環就可以獲得更小的值，會造成無法在有限步驟中獲得最佳路徑。