昨天我們使用預訓練模型EfficientNet去提取一張表情的高階特徵圖(1280張特徵圖),
今天,我們要用k-means將圖片特徵分群。
避免你忘了,下面的特徵都是來自這張原圖。
這1280張高階特徵圖,一定有其意義在。
而我們假設這些意義可以被歸類成k群,
那我們可以用手肘法決定出最佳k數!
其概念是先算出所有資料點與各群中心距離的平方和(Sum of Squared Error, SSE),
理論上,k=1時的SSE最大,k=N(資料點個數)時SSE為0。
所以隨著k提升,SSE就會下降。
雖然我們希望SSE變小,但k=N時明顯不合理(每個群都只有一個資料點= =)。
所以我們的判斷準則是:k提升到k_best時,SSE下降的趨勢開始不明顯。
而這就是手肘法取名的由來,
因為k提升到k_best時,SSE的下降斜率會從傾斜大幅轉為平緩。
SSE的程式碼實現:sum(np.min(cdist(X, X_mean, 'euclidean'), axis=1)) / sample_size)
sample_size, nrows, ncols = X_features.shape
X = X_features.reshape((sample_size, nrows*ncols))
distortions = []
K = range(1, 10)
for k in K:
kmeans = KMeans(n_clusters=k)
kmeans.fit(X)
distortions.append(sum(np.min(cdist(X, kmeans.cluster_centers_, 'euclidean'), axis=1)) / sample_size)
plt.plot(K, distortions, 'bx-')
plt.xlabel('k')
plt.ylabel('Distortion')
plt.title('The Elbow Method showing the optimal k')
for k in range(1, 9):
plt.text(k+0.65, 0.3, f"{distortions[k]-distortions[k-1]:.2f}",
bbox=dict(facecolor='green', alpha=0.5))
plt.show()
綠色框裡面的數字是k群的SSE與k-1群的SSE的相減,
可以發現k=5只比k=4下降了0.08,SSE斜率已經平緩。
所以最終決定k=4。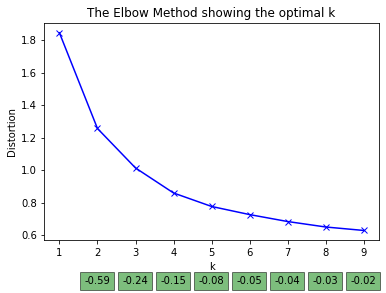
透過兩天的實作,
我想大家應該跟我一樣一頭霧水,
心裡想「我分出這四類特徵圖有甚麼用呢?我還是不知道其代表的意義啊!」
(雖然意義不好解釋,但這些特徵圖的確可以有效地讓神經網路分類器認識一張表情圖)
沒錯!
這就是分群方法的痛點:由於沒有標籤,各群的意義需要人們自己定義。
但是每個人的定義不同導致分群並沒有統一的標準。
而這個時候就需要資料科學家跳出來解決了。
其實除了手肘法,還有其他指標可以決定出最佳k數,
像是beale、gap、c index、gamma等。
有興趣的朋友可以將google這些關鍵字。
第 0 群特徵圖:
第 1 群特徵圖:
第 2 群特徵圖:
第 3 群特徵圖:

