梯度下降法經常被使用為優化學習的一種方式，尋找局部最佳解（至於為何是局部，之後會提到），想像有個半圓形的碗，在任何位置放入一顆球，那顆球就會在碗內滾動，每次滾動的高度都會越來越小，直到停在碗底。梯度下降法正是運用這樣的方式來計算，求出最佳解。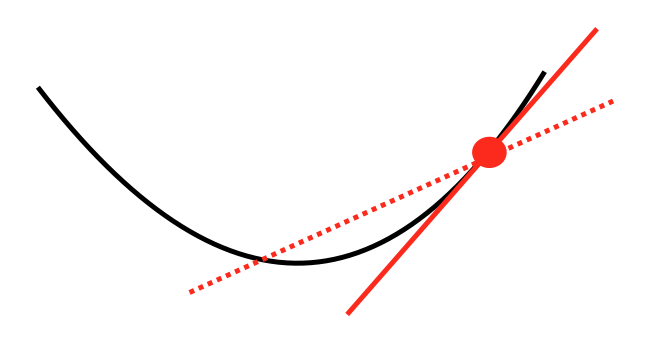

　　在原有的函式（也就是黑色曲線），隨機找到一個點，用微分的方式找到與這曲線的切線，目標是要把這切線變成水平線（也就是切線為零），因此發現這切線不為零的時候，接著調整切線的參數，計算曲線與切線相交的點，再慢慢調整直到找到最佳解。
　　但要注意切線的調整大小，如果調整幅度太大，可能會無法找到最佳解，一直卡在同一個地方，如下圖直接把切線調整為零，則永遠無法抵達最佳解。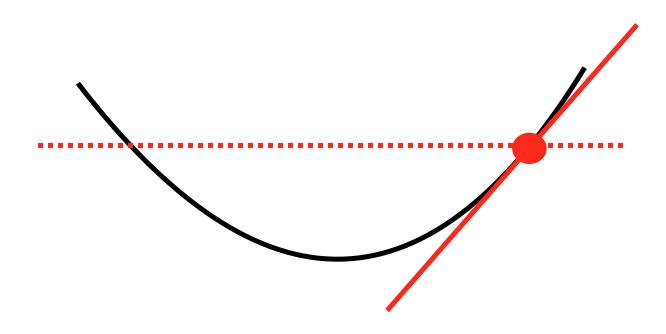

　至於為何只能找到局部最佳解，因為不可能剛好就只有一個凹下去的最佳解，如下圖，如果先找到了其中一個局部最佳解，就無法發現有更好的最佳解了，除非用其他資料測試的時候，有發現到原先的解並沒有那麼好，才有可能再做調整，因此為什麼機器學習要一直不斷的訓練，會比一次次更好，有一部份原因正是找到更好的局部最佳解。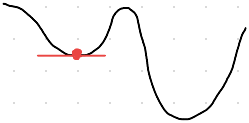

　另外，梯度下降法，如果剛好在坡度較為平緩，但並非最佳解的地方，也會使機器學習上頗有困難，如下圖。

　雖然梯度下降法仍然有些缺點，但只要透過不斷地訓練就避免陷入莫名的狀況，使得機器越來越好。