上一回講到兩種搜尋演算法，一種是一個一個找，一種則是每次尋找都可以去掉一半的選項，好像有一種是明顯比較快的做法，可是我們要怎麼表達這樣的差異呢？

執行時間

一般在選擇演算法時，我們會傾向用比較有效率的演算法，來優化時間或空間(例如記憶體)的運用，所以分析演算法時常常會討論其執行時間(running time)[註1]，也就是字面上執行一個演算法需要多少時間的意思。

通常執行時間會以演算法進行的基本操作(primitive operations)[註2]次數來衡量，並且寫法上利用大O符號(big-O notation)來表達。

以線性搜尋和二分搜尋來說，上回提到，用兩種方式來玩定時炸彈的話，最多分別要猜100次和7次。

所以假設輸入(例如數列、陣列長度或資料數量)為n時，線性搜尋最多需要進行n次操作，可以說線性搜尋的執行時間為O(n)，或稱為它具有線性時間(linear time)；二分搜尋最多需要log2 n次操作，因此執行時間為O(log n)，亦即代表二分搜尋具有對數時間(logarithmic time)。

換句話說，大O符號表達的執行時間，是演算法在最壞情況下的執行時間，也就是花最多步驟、最慢的狀態。

除了文字描述，我們還可以將這些關係用圖表示：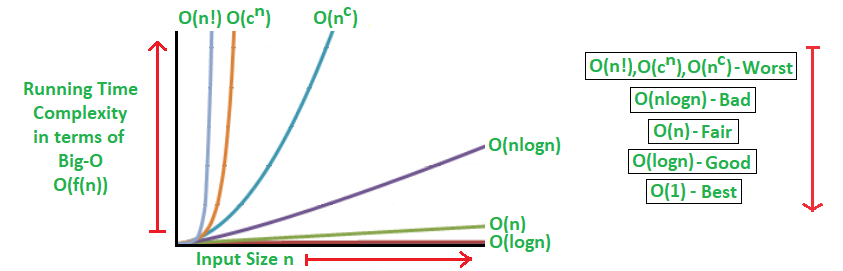

圖片來源 GeeksforGeeks

圖中x軸代表輸入大小，y軸代表所需時間(以操作次數衡量)，所以像圖中O(n)這條線，就代表具有線性時間的演算法(如線性搜尋)在輸入量變大時，它所需要的最長時間會如何增加。

這張圖中包含了一些常見的演算法執行時間，右側從上到下是最慢到最快的演算法比較，可以發現線條越陡(如O(n!))，演算法速度會越慢；線條越平(如O(log n))，則速度越快。

一路看名詞解釋到這邊，想必心中累績了很多疑問：

• 大O符號表達執行時間，那它有次或秒這類的單位嗎？
• 之前說二分搜尋最多要log2 n次操作，為什麼大O符號的寫法是O(log n)？這是寫錯還是省略？
• 為什麼一直以來都只討論演算法花最多時間的情況？

後續的文章會接著討論這些問題。

• [註1]如果看維基百科或一些文件可能會看到用時間複雜度(time complexity)這個詞來表示執行時間。不過目前在查詢相關資料的過程中，不管各種難度的課程或書籍裡，其實還是用執行時間表達居多。因為這個詞真的非常直接好懂，在認識演算法的一般討論階段我們會持續用執行時間這個表達。
• [註2]所謂基本操作是指演算法進行的一次簡單步驟(例如賦值、相加、比大小)。一次操作不一定等於一行程式碼，因為有些語言的語法在一行程式碼中即可以進行多次操作(例如檢查陣列裡的每個數字)。