數學方法去決定neuron輸出叫做激活函數(activation function)
但neuron的輸出並不是此方程式的結果,這是activation function對z值進行運算,並確定neuron的輸出。
Activation function會依據neuron的輸入是否與預測模組有關係,再來確定是否應執行activation function (打開或關閉)他所連接的neuron。實際上,activation function將每個neuron的輸出表準化為0到1或-1到1的範圍。
Linear Activation Function
線性激活函數根據函數將輸入乘以權重來計算neuron輸出。
線性激活函數的輸出由-∞ 到 +∞之間改變,這代表線性激活函數最好不要被啟動。
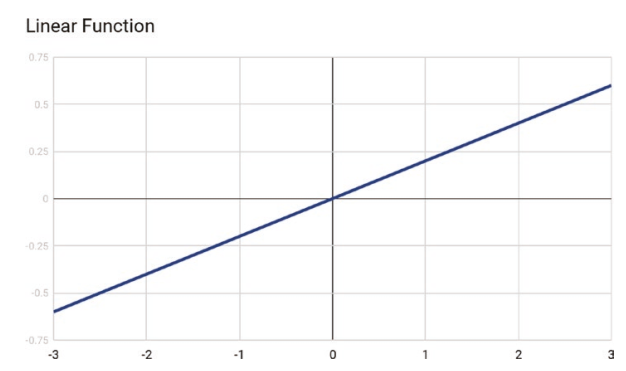
線性激活函數有以下兩種主要問題並且不在深度學習中使用:
深度學習使用一種叫做反向傳播(backpropagation)的方法,它使用了一種技術叫做梯度下降(gradient descent)的技術。梯度下降要求計算一階導數的輸入,在線性激活中是個常數(constant)。常數的一階導數為零,這代表它和輸入沒有任何關係。因此代表不可能回去更新輸入的權重。
假如使用線性激活方方法,無論神經網路層數是多少,最後一層將會成為第一層的線性函數。換句話說,線性激活函數將網路轉換成只有一層。這代表網路只能學習輸入到輸出的線性相依性,這並不適合解決電腦複雜的問題。
Sigmoid / Logistic Activation Function
Sigmoid activation function 使用S型函數計算neuron輸出。
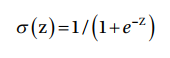
其中z使用的是之前方程式所得的值。
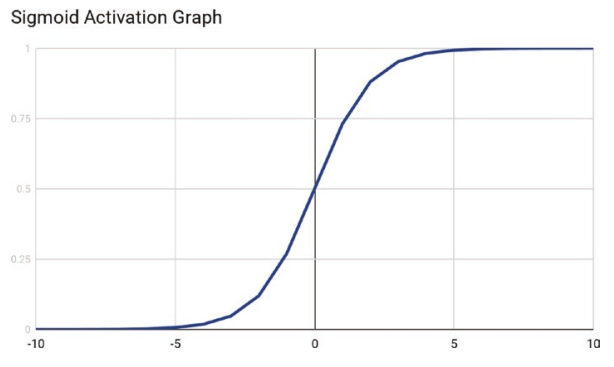
S型函數產生的值將會落於0到1之間,當輸入值大小有所差異時,將使得輸出平滑化,而不會出現數值差異過大的狀況。另一點優點是這是一格非線性函數且一階導數後不會產生常數值。這使得Sigmoid activation function相當適合使用於需要使用backpropagation的深度學習。
而sigmoid activation function最大的缺點就是輸出在大輸入值與小輸入值之間均不會有所改變。這使得sigmoid activation function不適合用於特徵向量包含大值或小值。一個克服這個缺點的解決方法是將特徵向量正規化,使得數值落於-1到1或者0到1之間。
另一個點是可以發現S型曲線並未居中於0。
我們下篇接續~
