上一次我們已經釐清了中央極限定理的概念了～不知道這樣的解說是否清晰？統計學其實是一個非常實用性的科學，如果不是建立在應用的基礎上，光是理解這些概念和理論非常難以消化和學習。希望透過這些概念性的回顧，重新幫大家建立起統計學的基礎知識，讓我們回到工作中，可以規劃出更具有統計上顯著的實驗！

如何開始你的假設檢定

在「如何開展你的分析？」中有談到，當我們定義好問題後，我要針對其原因進行驗證，而假設檢定便是你設立實驗的框架基礎。

假設檢定的步驟如下：

1. 設立虛無假設H0（Null Hypothesis）與對立假設H1（Alternative Hypothesis）
2. 選擇檢定統計量（test statistic）
3. 選擇顯著水準並決定決策法則
4. 比較樣本統計量與臨界值
5. 結論

我們在虛無假設為真的情況下進行推論，整個過程需要確定是否有足夠的證據來推翻虛無假設，也就是證明對立假設為真。因此如果有足夠的證據支持對立假設，那便是拒絕虛無假設，接受對立假設；反之，我們不拒絕虛無假設，也不接受對立假設。

為甚麼要特別強調不拒絕虛無假設，而不是說接受虛無假設？

打一個比方，以法官判案來說，我們的虛無假設H0是「被告無罪」，對立假設H1是「被告有罪」。如果我們有足夠的證據來推翻H0「被告無罪」，我們就可以證明對立假設H1「被告有罪」，但我們不會說我們接受H0「被告無罪」，而是因為沒有足夠的證據證明H1「被告有罪」，因此不拒絕H0「被告無罪」。

接受和不拒絕，兩者的概念並不一樣。

當我們在拒絕或是不拒絕虛無假設H0的同時，我們有可能會犯下兩種決策上的錯誤：型 I 錯誤 （Type I error）和型 II 錯誤 （Type II error）。

關於混淆矩陣

什麼是型 I 錯誤 （Type I error）？也就是我們拒絕的一個真實的虛無假設H0所會犯下的錯誤，沿用剛剛法官判案的例子，當一個真正無罪的人被我們宣判有罪時，便是型 I 錯誤 。

而型 II 錯誤 （Type II error）就是我們不拒絕一個錯誤的虛無假設H0，也就是一個有罪的人卻被宣判無罪釋放。

換一個現在我們比較熟悉的說法，大家應該都有聽過偽陰性和偽陽性吧？

虛無假設H0為沒有感染，對立假設H1為感染。

偽陽性就是明明沒有感染，我們確判斷他確診，型 I 錯誤 （Type I error）；反之偽陰性就是明明有感染，我們確判斷他沒有問題，型 II 錯誤 （Type II error）。

是不是漸漸地覺得有點混亂了呢？那我們再來看看這一張表！

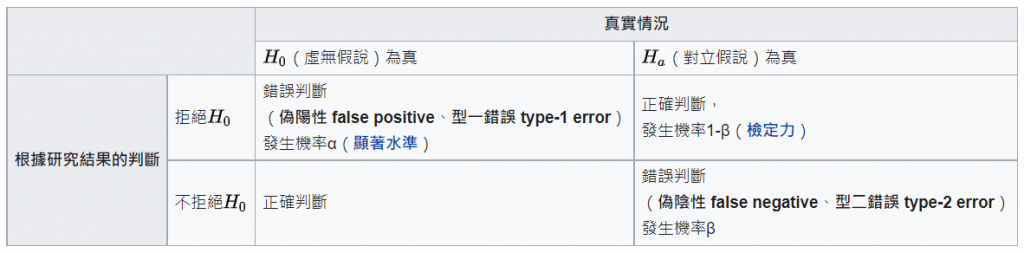
＊圖片來源自維基百科

有沒有比較清楚呢？還是感覺更換亂了（笑）。

而在機器學習中，評估模型好壞的時候也很常會用到傳說中的混淆矩陣（confusion matrix），其原理就是所謂統計學上的型 I 錯誤和型 II 錯誤。

TP（True Positive）： 正確預測成功的正樣本。

TN（True Negative）： 正確預測成功的負樣本。

FP（False Positive）： 錯誤預測成正樣本，實際上為負樣本，所謂的誤抓，型 I 錯誤。

FN（False Negative）： 錯誤預測成負樣本，實際上為正樣本，所謂的漏抓，型 II 錯誤。

不愧是混淆矩陣！看到這邊原本覺得自己會了都變成不會了呢！

呼～～～今天我們花費了極大的篇幅和大家建立假設檢定的一些基本觀念以及需要認知到可能會犯的錯誤（好累），接下來我們要來看關鍵的檢定統計量、顯著水準以及檢定力～

參考資料：

型一錯誤、型二錯誤

https://zh.wikipedia.org/wiki/型一錯誤與型二錯誤

https://highscope.ch.ntu.edu.tw/wordpress/?p=73236

混淆矩陣

https://www.ycc.idv.tw/confusion-matrix.html

延伸閱讀：

https://web.ntpu.edu.tw/~stou/class/ntpu/CH11-Keller-in-Chinese-2011.pdf

https://web.ntpu.edu.tw/~wtp/statpdf/Ch_10.pdf

http://www1.pu.edu.tw/~hdchen/handout_bank/stat/94_4_stat_handout_06.pdf