Graph(圖)顧名思義它是跟圖有關的資料結構(廢話)。

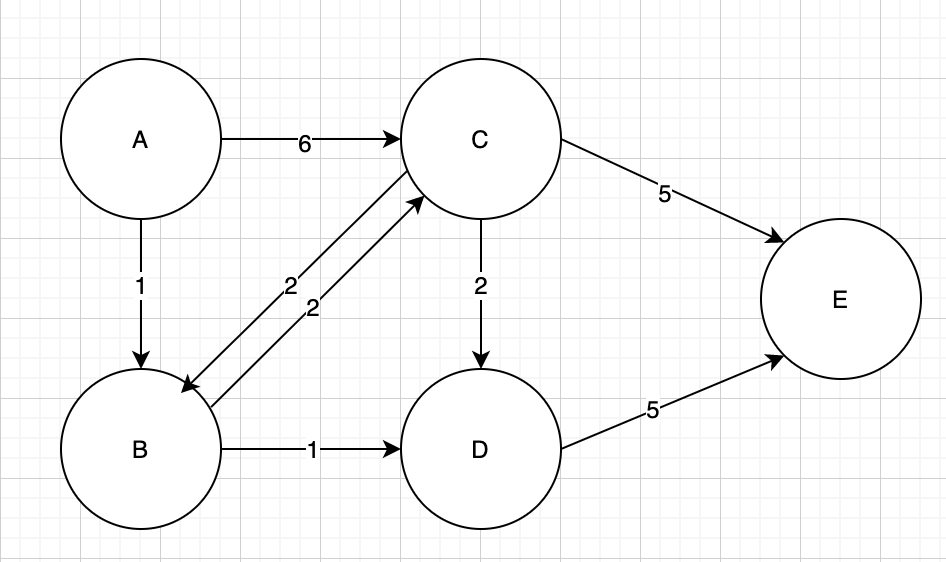
A~E我們會稱為頂點(Vertex)，每一個頂點之間的是線(Edge)，當線是有方向的我們會稱這是有向圖(Directed graph)，如果沒方向就代表兩個頂點相通，那就叫無向圖(Undirected graph)。
邊上的數字代表距離，A到C要6km，A到B要1km...
Graph可以用來儲存地圖或者關係流程，例如把A~E轉成人物，邊的值存下他們的關係，A認識B、C，B跟C相互認識....

那我們要怎樣去用儲存這些資料的關係?
今天會介紹Adjacency list的資料構結，比較常見的還有Adjacency matrix跟Edge list，每一種資料結構都有點不一樣。因資料構結的類型，在不同的算法底下，時間複雜度會有差別，這邊就不一一介紹了～

Adjacency list

來看一下資料結構

// 頂點
type Vertex struct {
	Name string
}

// 邊
type Edge struct {
	Vertex   *Vertex
	Distance int
}

// 圖
type Graph struct {
	adjList map[*Vertex][]*Edge
}

Graph裡面的adjList是一個map，用來存放圖的資料，map裡面的Key是每一個頂點，Val是一個slice用來存該頂點的每一條邊(slice你也可以用鏈結來取代哦)。

最後map看起來會長這樣

A: [B,C]
B: [C,D]
C: [B,D,E]
D: [E]
E: []

剩下來就把程式的function都補上去

// 新增頂點
func (g *Graph) AddVertex(node *Vertex) {
	g.adjList[node] = []*Edge{}
}

// 新增邊
func (g *Graph) AddEage(a *Vertex, b *Vertex, distance int) {
	g.adjList[a] = append(g.adjList[a], &Edge{
		Vertex:   b,
		Distance: distance,
	})
}

// 把頂點跟邊都print出來
func (g *Graph) Show() {
	for vertex, edges := range g.adjList {
		str := vertex.Name + " -> "

		for _, edge := range edges {
			str += edge.Vertex.Name + " "
		}

		fmt.Println(str)
	}
}

func newGraph() *Graph {
	return &Graph{
		adjList: map[*Vertex][]*Edge{},
	}
}

來加入頂點跟邊

func main() {
	a := &Vertex{
		Name: "A",
	}
	b := &Vertex{
		Name: "B",
	}
	c := &Vertex{
		Name: "C",
	}
	d := &Vertex{
		Name: "D",
	}
	e := &Vertex{
		Name: "E",
	}

	g := newGraph()
	g.AddVertex(a)
	g.AddVertex(b)
	g.AddVertex(c)
	g.AddVertex(d)
	g.AddVertex(e)

	// A的邊
	g.AddEage(a, b, 1)
	g.AddEage(a, c, 6)
	// B的邊
	g.AddEage(b, c, 2)
	g.AddEage(b, d, 1)
	// C的邊
	g.AddEage(c, b, 2)
	g.AddEage(c, d, 2)
	g.AddEage(c, e, 5)
	// D的邊
	g.AddEage(d, e, 5)

	g.Show()
}

output:

A -> B C 
B -> C D 
C -> B D E 
D -> E 
E -> 

今天介紹完圖的資料結構，明天後天會講DFS、BFS～