DFS是簡寫，全名是Depth-First-Search(深度優先搜尋演算法)
DFS是一種搜尋的算法，在不同的資構結構都會看到，是一種很常見的算法哦！

先來看一下圖: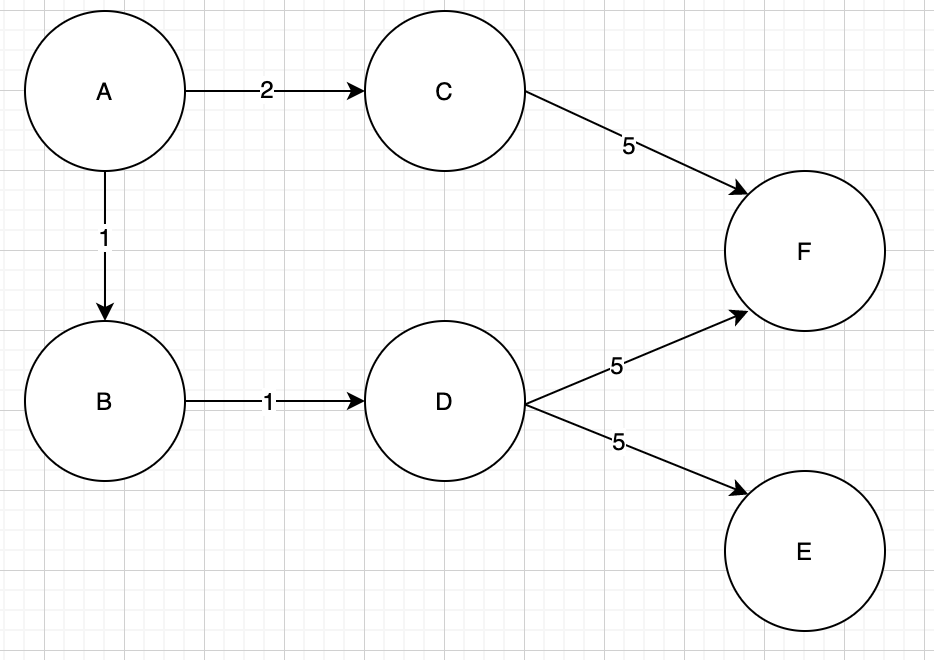

如果我們要找出A點可到達的其他頂點要怎麼做？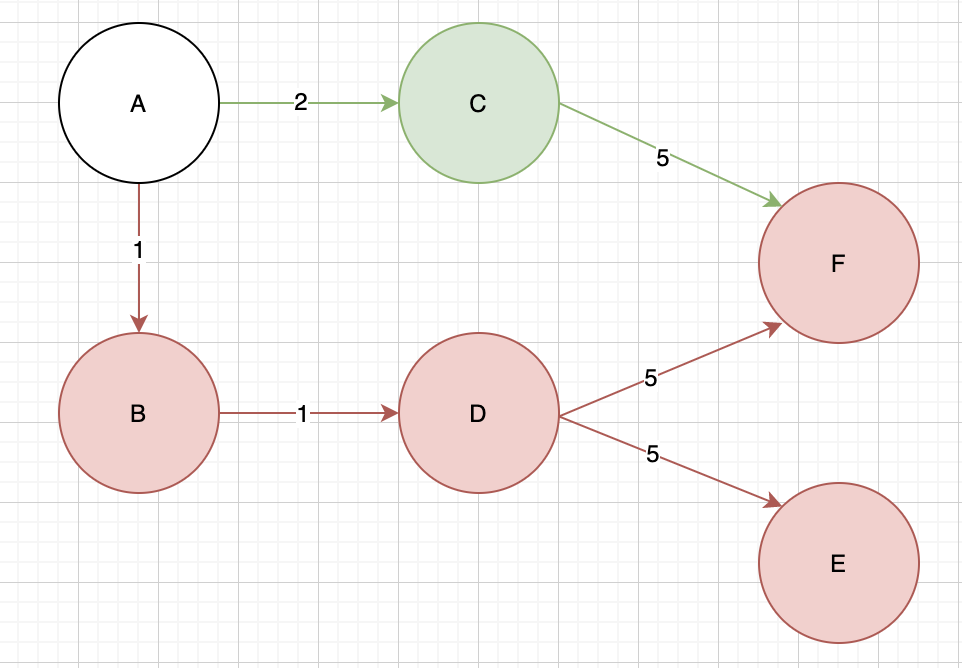

我們以A點為起點，每一條邊線都一直往下走，直到盡頭，再去走其他線邊。
紅線是第一次尋找，A第一條邊是通往B的，直接順著走到底，到E就沒路可走了，回到D點的第二條邊走到F，路徑為A->B->D->E->F。
當到F沒路去，A會走第二條邊通往C(綠線)，一樣走到底，A->C，當走到E的時候，會發現E之前就來過了，所以停下了，A也沒有第三條邊可以走，結束搜尋。
直接看圖解理解起來應該不難，把它轉成程式～

程式:

// 回傳全部的頂點
func (g *Graph) getVistedVertex() map[*Vertex]bool {
	visted := map[*Vertex]bool{}
	for v := range g.adjList {
		visted[v] = false
	}

	return visted
}

func (g *Graph) DFS(target *Vertex) {
	visted := g.getVistedVertex() // 用來記錄走過的頂點
	visted[target] = true

	g.dfsRecursive(target, visted)
}

// 算法核心用遞迴的方式來做
func (g *Graph) dfsRecursive(vertex *Vertex, visted map[*Vertex]bool) {
	for _, edge := range g.adjList[vertex] {
		// 判斷之前有沒有來過
		if !visted[edge.Vertex] {
			// 走過的點要記錄下來，不然可能會無限迴圈
			visted[edge.Vertex] = true
			fmt.Printf("vist: %v \n", edge.Vertex.Name)
			// 繼續遞迴往下走
			g.dfsRecursive(edge.Vertex, visted)
		}
	}
}

func main() {
	a := &Vertex{
		Name: "A",
	}
	b := &Vertex{
		Name: "B",
	}
	c := &Vertex{
		Name: "C",
	}
	d := &Vertex{
		Name: "D",
	}
	e := &Vertex{
		Name: "E",
	}
	f := &Vertex{
		Name: "F",
	}

	g := newGraph()
	g.AddVertex(a)
	g.AddVertex(b)
	g.AddVertex(c)
	g.AddVertex(d)
	g.AddVertex(e)
	g.AddVertex(f)

	// A的邊
	g.AddEage(a, b, 1)
	g.AddEage(a, c, 2)
	// B的邊
	g.AddEage(b, d, 1)
	// C的邊
	g.AddEage(c, f, 5)
	// D的邊
	g.AddEage(d, e, 5)
	g.AddEage(d, f, 6)

	g.DFS(a)
}

output:

vist: B 
vist: D 
vist: E 
vist: F 
vist: C

明天來講BFS~