昨天說明了為什麼會想使用Elo Rating 作為戰力估計的原因
因為可以把作答者的作答結果
視為作答者與題目之間的比賽結果
再藉由此結果估計作答者戰力
接下來說說它的更新公式

以答對率估計題目戰力

在前天介紹IRT的三參數中
提到了三參數分別代表了「難度」、「區分度」、「猜測度」
但是其中的難度、區分度較難被估計
通常需使用聯合最大概似估計
但計算量通常較大

如剛剛所說
若我們把作答者答題視為作答者與題目的比賽
則是否即可利用題目的答對率作為題目戰力的估計
並回推估計作答者的戰力呢

在文獻[1]中有提到當隨機選題時
答對率可以提供不錯的題目難度估計
因此應可直接使用
(若不使用答對率也可，把題目難度從0開始進行估計)

更新公式

先講文獻中的原文更新公式

文獻中為從0開始同時更新並估計題目難度及作答者戰力
作答者答對機率為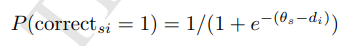

其中 表示作答者戰力， 表示第 i 題難度

可依照其作答情形(答對為1，答錯為0)做以下戰力更新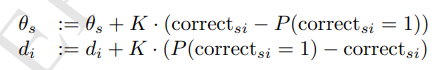

題目難度與學生戰力初始值皆為0
其中 K 為敏感參數，太小不容易收斂，太大又不夠穩定，詳情可參考文獻

但我在這裡選擇直接用答對率作為題目難度估計
定義 題目難度 = 1 - 答對率 (答對率越低，則題目難度越高)
且不再更新題目難度
其餘公式如上，唯更新時僅更新學生戰力而已

所以現在可以利用Elo 來估計學生戰力了
下一步就是把它寫成gogole script 啦~

參考文獻：
[1] Pelanek R., Applications of the Elo Rating System in Adaptive Educational
Systems, Computers & Education (2016), doi: 10.1016/j.compedu.2016.03.017