今日題目

題目連結：965. Univalued Binary Tree
題目主題：Tree, Depth-First Search, Breadth-First Search, Binary Tree

Traversal 除了在 Depth-First Search 中會看到的Preorder、Inorder、Postorder以外，另外還有一種叫做Level-Order Traversal，通常在Breadth-First Search主題中使用到。

簡單說說 Level-Order Traversal

Level-Order Traversal通常會在Breadth-First Search主題中看到，原則就是以層級的方式一層一層往下讀取，運作過程如下圖：

假設資料是 tree = [5, 2, 6, 1, 3, null, 8]

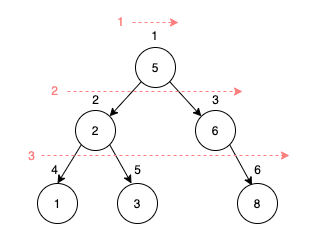
上圖中，每個節點上面的數字是讀的順序，而紅色虛線箭頭就是讀的方向。這邊滿單純的，可以看到就是從最上層，一層一層照順序讀下來，Level-Order排出來順序就會是 [5, 2, 6,1, 3, 8]，通常會使用Queue來實作，若還沒了解過Queue的夥伴建議也可以先看看本系列文 Day 6：232. Implement Queue using Stacks 的簡單說說 Queue。

題目解說

建議可以看看LeetCode原本的題目說明，這邊是用我的方式說明題目，參考就好。

本題會給一顆二元樹，目的是要確認，這棵樹的所有節點是否全部都是同樣的一個值，如果全部節點的值都一樣會回傳True，只要有一個值不同，就會回傳False。

約束：

• 樹的節點總數範圍在 [0, 100]
• 0 <= Node.val < 100

範例1

輸入：root = [1,1,1,1,1,null,1]
輸出：true
解說：可以看到輸入的樹，全部都是1，所有的節點值都相同，因此回True。

範例2

輸入：root = [2,2,2,5,2]
輸出：false
解說：輸入的樹中幾乎都是2，但其中出現了一個 5，有節點的值不一樣，因此回False。

建議到這邊先停下來，嘗試自己解解看，若沒有想法可再繼續走下去。

解題的想像

文字描述

1. 把根節點的值先記錄下來，用來判斷每個節點是否為相同值。
2. 宣告一個Queue來實作Level-Order Traversal。
3. 將根節點先放入Queue中。
4. 跑一個迴圈，直到每個節點都走過一次：
   • 每一圈都會取得目前讀到的節點。
   • 將目前節點的值跟第 1 步驟記錄的根節點值確認是否相同。
   • 若不同直接回傳 False 結束，代表這棵樹已經不是全部節點的值都相同。
   • 若相同繼續確認是否還有節點，如果還有節點，將節點都放進Queue繼續迴圈。
5. 若全部節點都相同，回傳True結束。

圖解過程

範例：root = [5, 5, 5, null, 4]

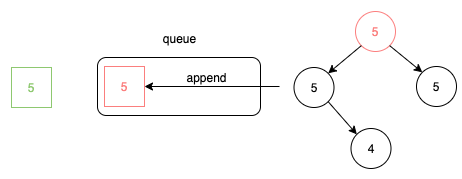
上圖中，綠色方框是一開始要紀錄的根節點值，也是用來跟之後每個節點值確認是否相同的值。而中間的Queue就是用來實作 Level-Order Traversal用的，在這邊已經先把根節點放進去了。

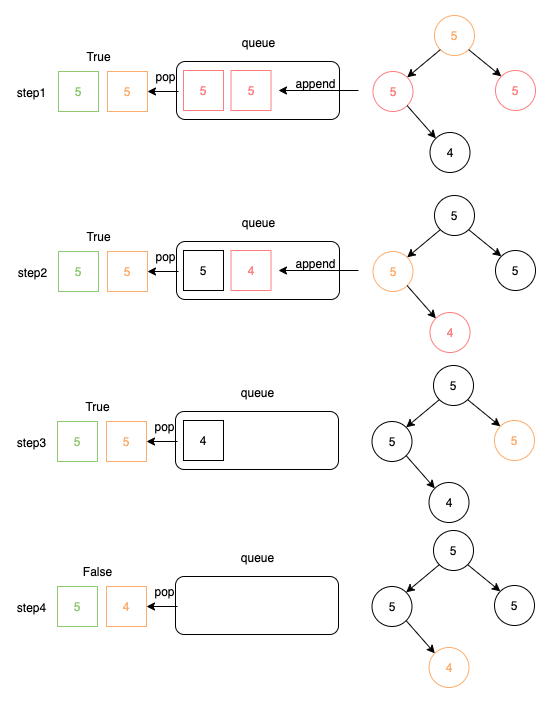
上圖是迴圈運作的過程，每一圈都會取得一個橘黃色方框，這個橘黃色方框是目前讀到的節點，而紅色方框就是橘黃色方框的子節點，會先放進Queue中預備。

每一圈都會檢查目前的節點的值跟綠色方框根節點的值是否相同，若相同會繼續走下去。另外可以看 step3 及 step4，因為目前讀到的橘黃色方框都沒有子節點，所以不用作append的動作。step4 這個步驟也檢查到有節點的值與根節點值不同，因此這個範例的結果會回傳 False。

最後也可以觀察一下 step1 ~ step4 的橘黃色方框，讀的順序就跟前面分享 Level-Order Traversal 走的順序是相同的，這就是用 Queue 實作 Level-Order Traversal 的過程。

若因為沒想法而走到這邊，建議看完想像以後再給自己一次機會試一次。

程式碼撰寫

class Solution:
    def isUnivalTree(self, root: Optional[TreeNode]) -> bool:
        # 紀錄根節點的值
        value = root.val
        # 使用Queue來實作 Level-Order Traversal
        queue = deque()
        # 從根節點開始讀
        queue.append(root)
        
        # Queue 走到 0 代表全部節點都讀過
        while len(queue) > 0:
            # 每圈讀取一個節點
            node = queue.popleft()
            # 檢查這個值是否與根節點值不同，若不同直接回傳False結束
            if node.val != value:
                return False
            # 若還有子節點，放進Queue，讓迴圈繼續走完每個節點
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)

        return True

希望您今天能瞭解到...

1. Level-Order Traversal
2. 965. Univalued Binary Tree 的解題方法

若內容有什麼問題或建議歡迎一起交流：）
感謝您今天願意花時間看完這篇文章~~~~

Next：101. Symmetric Tree