深度優先搜尋(depth-first search, DFS)是一種搜尋整張圖所有節點的演算法。它的名稱也表達出跟廣度優先搜尋的順序不太一樣，它是從根節點(樹的情況)，或任意節點(圖的情況)開始，盡可能搜尋所有可以抵達的子節點，直到分支的盡頭、沒有子節點的地方，再回溯進行同樣的搜尋。

以下圖為例，節點上的數字即為深度優先搜尋的順序。從根節點1開始，檢查其中一個尚未檢查的子節點2，並持續檢查子節點的子節點，直到沒有子節點的4為止再回頭。回溯的方法是回到上一個有子節點的分支，例如4回溯到3，並檢查3的另一個子節點5。

圖片來源：維基百科

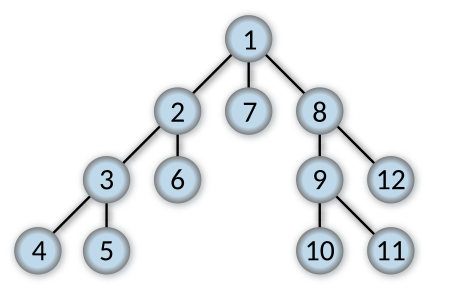
雖然一樣是搜尋所有的節點，但這樣的順序讓深度優先搜尋可以應用在不同地方，其中一個就是拓樸排序(topological sorting)。

拓樸排序

拓樸排序是指將一個有向圖的節點排序，方式是如果兩節點之間邊的方向是u到v，則在排序中節點u會在節點v前面。

例如說下圖中節點7和8的方向是7到8，所以在拓樸排序中7一定出現在8前面。一張圖不一定只有一種拓樸排序，例如這張圖的一種排序可以是5, 7, 3, 11, 8, 2, 9, 10，也可以是3, 7, 8, 5, 11, 9, 10, 2。

圖片來源：維基百科

如果直接對這張圖進行深度優先搜尋，並依搜尋順序將節點加入陣列中，並不會得到拓樸排序的結果(例如從5開始深度優先搜尋的話11會在7前面，但拓樸排序7應該在11前面)。但我們可以稍微改變方式，來進行拓樸排序。

方法是：從任一節點開始，用遞迴的方式進行深度優先搜尋，直到沒有子節點或到達已經搜尋過的節點，再將搜尋過節點加到堆疊中。

例如從8開始深度優先搜尋，到子節點9後沒有子節點，所以將節點加入堆疊中
stack = [9, 8]

接著從5開始深度優先搜尋，搜尋的節點為5, 11, 2, 10 (9已經搜尋過)，將節點加入堆疊中
stack = [9, 8, 10, 2, 11, 5]

接著搜尋7，子節點都已搜尋過，將7加入堆疊中
stack = [9, 8, 10, 2, 11, 5, 7]

最後搜尋3，子節點都已搜尋過，將3加入堆疊中
stack = [9, 8, 10, 2, 11, 5, 7, 3]

過程中搜尋到分支的終點才將節點加入堆疊，而非每搜尋一個就加入一次，這樣確保每條分支的節點順序。最後因為堆疊後進先出的原則，輸出後可以得到拓樸排序的數列[3, 7, 5, 11, 2, 10, 8, 9]。

應用

那麼，拓樸排序可以用在什麼情境呢？我們可以把節點的有向邊想成表達事情之間的先後關係。例如有向邊ab，可以代表a任務有優先性，或必須先完成a任務才能完成b任務，而拓樸排序既是以邊的方向排序，自然就可以用來代表任務順序。

實際例子就好比大學會對某些課程有擋修的規定。例如學生必須上完化學1才能上化學2，另外必須修完微積分1才能修微積分2，但化學1和微積分1之間就沒有順序的限制。若課程之間有類似這樣關係，則所有課程的拓樸排序就是一個可行的修課順序。