生活上我們可能有遇過一些二分搜尋的例子。
例如以前如果有當過助教的經驗，有時候我們在收學生作業時會作業按照學號由小到大排好，
假設有100位學生001~100，我們要找第69號，我們可能會大概拆分成兩疊在從後面那一疊，而非從頭開始慢慢算，這就是二分搜尋的生活例子！

從這個例子中可以發現，如果我們今天要從已經排列好的東西找到想要的結果
→ 我們都可以想想二分搜尋是否可以派上用場！

那我們來看看這題題目吧！

Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4

今天拿nums = [-1,0,3,5,9,12] ，我們想要尋找9是否在nums內，如果有救回傳他的index，沒有則回傳-1。
一開始我們要出中位數的index，我們先建立一個左指標和右指標分別指向nums的頭和尾，計算中間值index。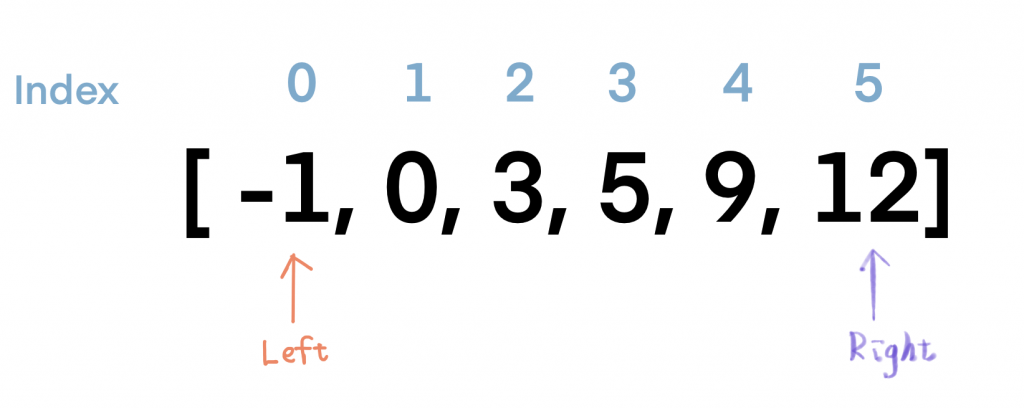

(0+5)/2 無條件捨去法，得到2。
我們得到 nums[2] 為 3，又因 3 < 9 ，所以我們知道9的index一定是在2的右手邊
於是我們就可以忽略 index 從 0 到 ２的元素！直接從 index=３開始尋找，所以我們把左指標移到了 nums[3]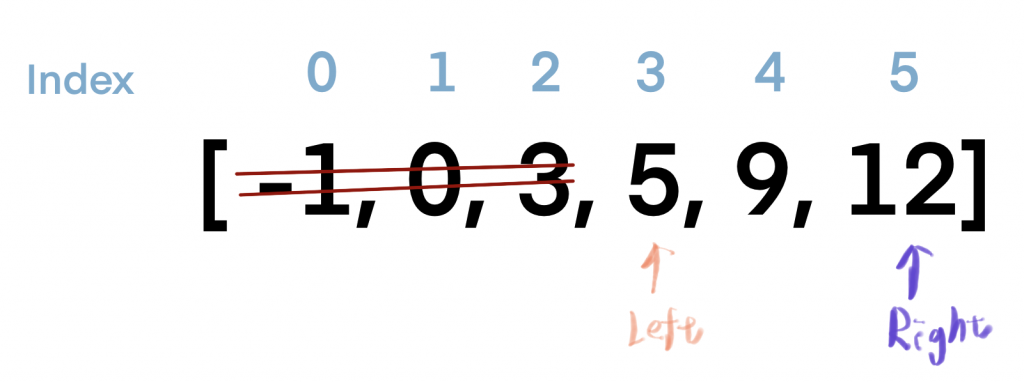

一樣找中間index
( 3 + 5 ) / 2 = 4
nums[4] = 9 於是我們找到了9的index為4

以上就是二分搜尋。

那如果我們要尋找的數不在陣列中會發生什麼事？
我們一樣用同樣得陣列來尋找 target = 10
我們接著nums[4] = 9，所以10的index一定會在4的右手邊。
我們要把左指標移到index為5的位置，這時候發現左邊跟右邊的指標指向同一個位置了！
但是 nums[5] = 12≠10 對吧？
又因為 10 < 12
這時候我們想要把右指標移動到 index 為 5 - 1 = 4
但這樣卻變成右邊指標跑道左邊指摽的左手邊了！
這時我們就可以理所當然地停止搜尋，也就是這個數根本存在！
時間複雜度為 O(logN)
空間複雜度方面，則牽涉到我們的實作方式有關。

如果是用iteratively的方式，Space可以為O(1)，只需要紀錄中間index
如果是recursively的方式，用到stack的資料結構，就會讓Space變成O(logN)

讓我們來看一下兩種方式的實作吧！

// iteratively
var search = function (nums, target) {
  return binarySearchMethod(nums, target, 0, nums.length - 1);
};

const binarySearchMethod = (array, target, left, right) => {
  while (left <= right) {
    const midIndex = Math.floor((left + right) / 2);
    const midNumber = array[midIndex];
    if (target === midNumber) {
      return midIndex;
    } else if (target < midNumber) {
      right = midIndex - 1;
    } else {
      left = midIndex + 1;
    }
  }
  return -1;
};

//recursively

var search = function (nums, target) {
  return binarySearchMethod(nums, target, 0, nums.length - 1);
};
const binarySearchMethod = (array, target, left, right) => {
  if (right < left) return -1;
  const midIndex = Math.floor((left + right) / 2);
  const midNumber = array[midIndex];
  if (target === midNumber) {
    return midIndex;
  } else if (target < midNumber) {
    return binarySearchMethod(array, target, left, midIndex - 1);
  } else {
    return binarySearchMethod(array, target, midIndex + 1, right);
  }
};

明天題目預告： 二元樹的三種走訪 BST Traversal