今天一起來認識二元樹的三種遍歷方式吧！
但是別急！我們先來認識二元搜尋樹BST的定義！

二元搜尋樹是一棵二元樹，如果不為空（二元樹可以為空！）
則須滿足:

1. 左子樹所有節點(Nodes)的值都要小於Root
2. 右子樹所有節點(Nodes)的值都要大於或等於Root
3. 它的左右子樹也都要是BST
   

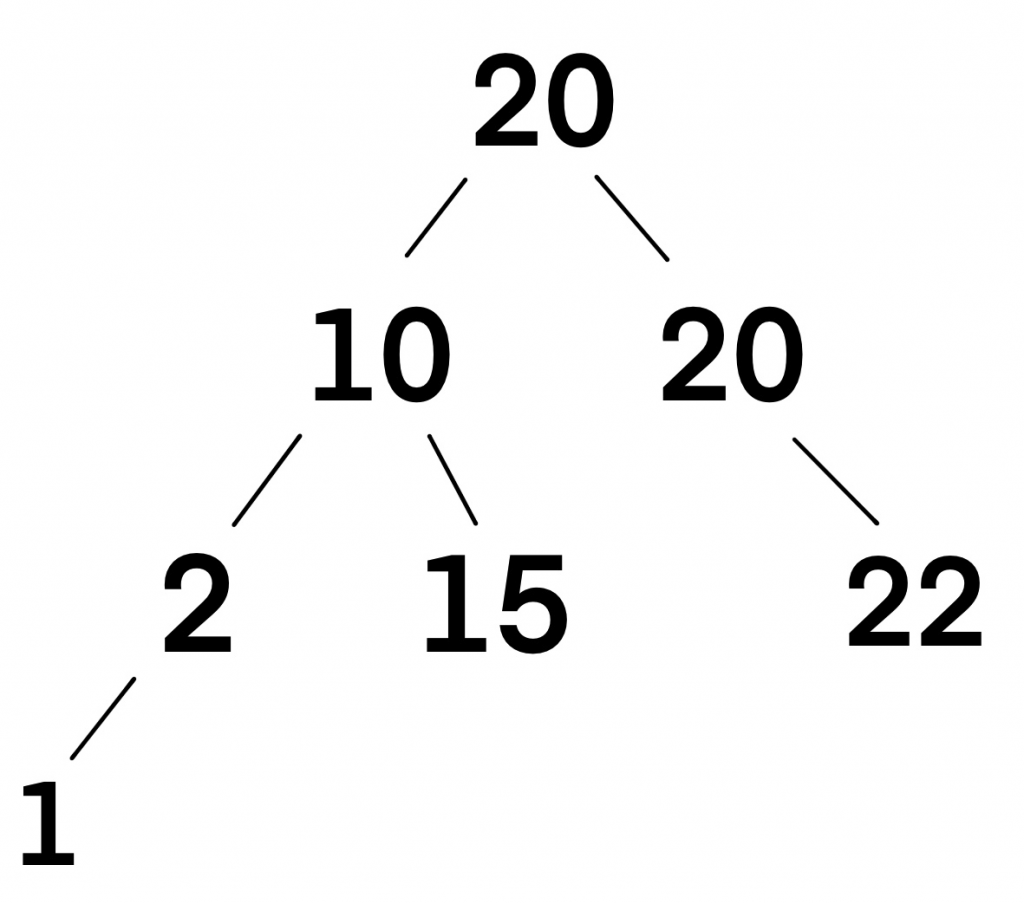
我們以這張圖為例
我們預期三種不同的結果如下

1. 中序 In-order: [1, 2, 10, 15, 20, 20, 22]
2. 前序 pre-order: [ 20, 10, 2, 1, 15, 20, 22]
3. 後序 post-order: [1, 2, 15, 10, 22, 20, 20]

我們可以從結果觀察到：中序追蹤可以恰好得到由小到大排列好的結果！
中序的行為其實就是 “左中右”的感覺
同理
前序 → 中左右
後序 → 左右中
也就是說
"中"就是我們當下拜訪到的當下結點，"左"就是左兒子（left child），"右"則是右兒子
有沒有發現這三個名稱其實是跟去“中”在前中後下去命名的感覺(我都是這樣記的～)

而它程式碼的實現也會是依照著個邏輯下去走！
像是中序追蹤，其實就是：

inOrderTraverse(left)
array.append(current.value)
inOrderTraverse(rigtht)

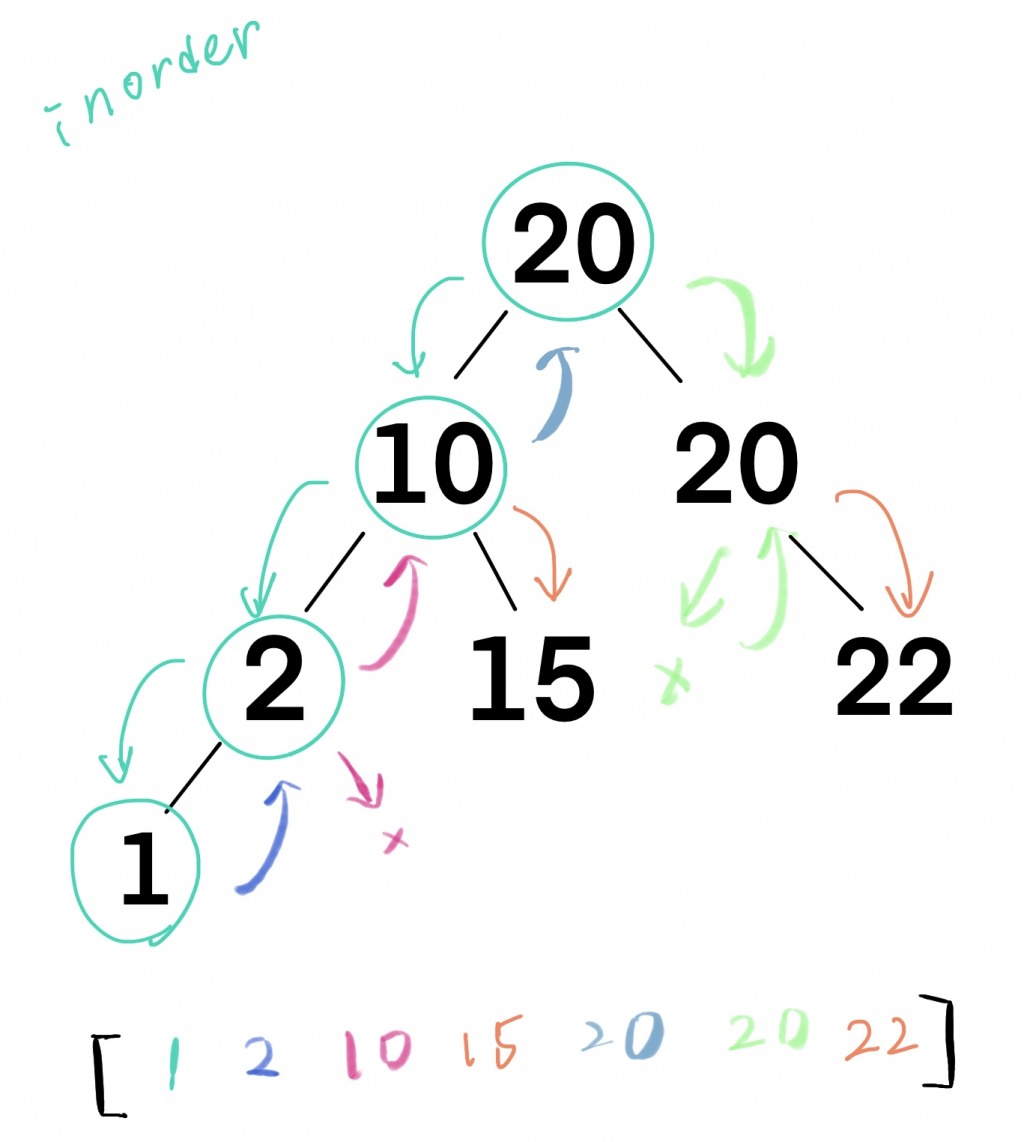
以這張圖為例，我們一開始從20開始不斷往左邊走到1，而後發先1沒有左子樹和右子樹，我們就把他加到陣列。
接著退回2，並把2加到陣列，發現2沒有右子樹又退回去2，繼續類似的路徑，再退回去10...以此類推。這就是中序追蹤的行為！

規則講到這裡我們來挑戰題目吧！

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
    
function inOrderTraverse(tree, array) {
  if(tree !== null ){
		inOrderTraverse(tree.left, array);
		array.push(tree.val);
		inOrderTraverse(tree.right, array);
	}
	return array;
}

var inorderTraversal = function(root) {
    const array = [] ;
    if(!root) return array;
    inOrderTraverse(root,array);
	return array;
};

做完inorder的題目，別忘了自己推一下preorder以及postorder，也都是leetCode裡面的題目喔！
今天等於完成了三題！
下面作法

function preOrderTraverse(tree, array) {
    if(tree !== null ){
		array.push(tree.value);
		preOrderTraverse(tree.left, array);
		preOrderTraverse(tree.right, array);
	}
	return array;
}

function postOrderTraverse(tree, array) {
  if(tree !== null ){
		postOrderTraverse(tree.left, array);
		postOrderTraverse(tree.right, array);
		array.push(tree.value);
	}
	return array;
}

明日預告： 認識了前中後序的走訪，來試試實作深度追蹤吧！