深度追蹤是刷題前一定要了解的觀念！
今天就來用Depth-first-searh的方式來走訪一棵樹吧！

其實從名稱上看起來很直覺，簡單來說就是當我們走了一條路，前面有多深我們就一直往更深的路走下去，也就是我們會不斷探索特定的路直到沒有路可以走為止，而後才回退到我們經過的岔路再繼續重複的深度探索。

同樣情形換作是探索一棵樹，我們就一直循著他的樹根，不斷往更深的地方走，如果遇到分岔，一樣要不斷往下走(先左後右)，和廣度追蹤Breadth-first-search不同（BFS是層級上的追蹤，明天回提到！)

參考下面這張圖，我們會先走
A → B → E 發現沒路，退回Ｂ
B → F → I 又沒路了，退回Ｆ
F → J 又沒路，退回F，F有的路都走過了，再回B ....以此類推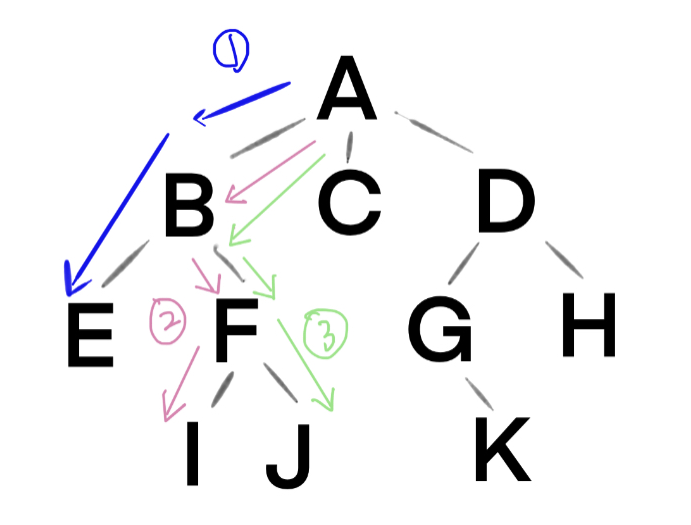

從上面的狀況，我們可以發現拜訪的方式都一樣 → 想到遞迴。
也就是我們不斷去呼叫同一個函式做一樣的操作！

所以我們來想想，
如果我們把拜訪過的節點放到陣列，重複回退的就不再放入，這個陣列會長什麼樣子？
是不是[A, B, E, F, I, J, C, D, G ,K ,H]？

當然不免俗的要提一下時間複雜度 Time: O(V+E)
其中 V : node數，E: edge(邊數，像是如圖A-B之間的一條線，就是one edge)，也就是說Ｅ的數量就是node間連接的數量。
換句話說：每當我們拜訪一個節點，我們就把他加到陣列。
也就是說，我們拜訪到一個node，就要呼叫一次function，
但是呼叫function之後，這個node又有幾個相連岔路（edge）要呼叫這個function。
像是A就有3個小朋友 ，但 H 就都沒有小朋友。

那空間複雜度呢？ 答案是Ｏ(V)
因為過程中，我們不斷把每個點推到Stack（如下）：
在 D 之前我們要先執行完 H, K, G 的呼叫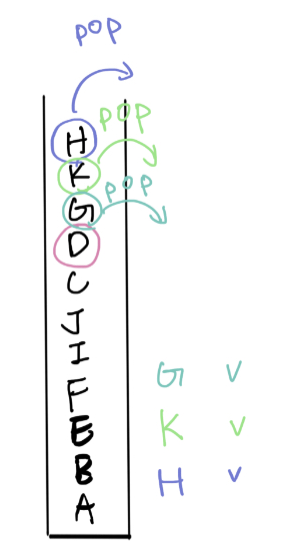

考慮最糟的情況，例如左偏樹，我們一樣要把他依序推到stack並一個個執行，而且我們的陣列長度其實也是節點數目。

最後來看看程式碼的實作！

class Node {
  constructor(name) {
    this.name = name;
    this.children = [];
  }

  addChild(name) {
    this.children.push(new Node(name));
    return this;
  }

  depthFirstSearch(array) {
    //先把目前拜訪的node加到array
    array.push(this.name);
    //繼續拜訪此node的孩子們 每個孩子都要call depthFirstSearch
    for (const child of this.children) {
      child.depthFirstSearch(array);
    }
    return array;
  }
}

明天題目預告：廣度追蹤之應用 Binary Tree Level Order Traversal