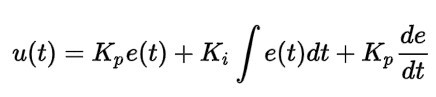前言

這裡要先聲明，我沒有修過專業的控制相關課程，如果想要學習更專業的PID相關內容可能這裡不適合，我只是將我這個暑假所研究的成果記錄下來分享給大家，對於最基礎的馬達控速應該是沒問題啦。

PID是什麼?

PID是「控制方法」，是根據目前狀態與預設值的偏差值，按比例、積分、微分等運算，運算結果用以輸出來進行控制。以馬達來說，我們需要的是馬達以一個恆定的速度轉動，因此先透過之前介紹過的encoder(編碼器)，來得知目前的轉速，再以上述的運算，最後根據計算的結果來輸出電壓。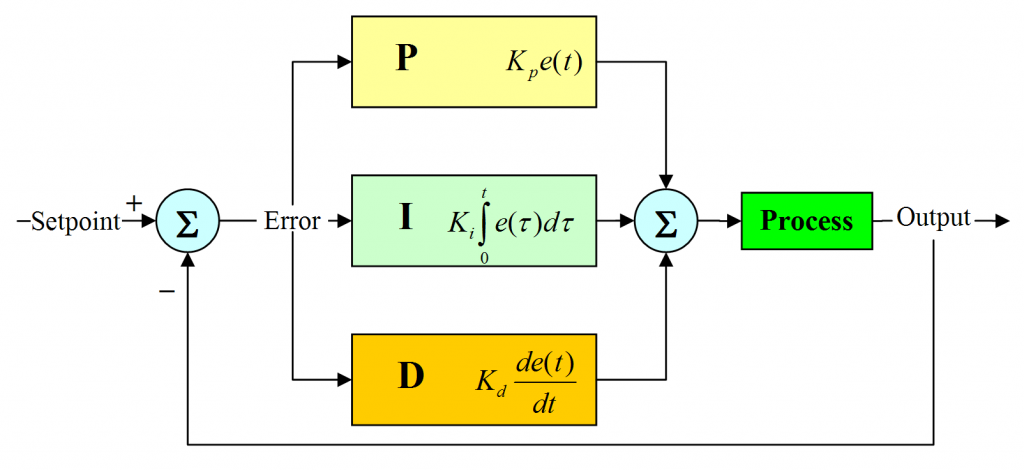

控制方法

我們先不要管PID，我們來想想看：假設要控制房間到一個恆定的溫度20度，冷氣應該要怎麼設定？(假設室溫30度)
思路如下：
起初為了讓室溫快速降低，可以先開冷一點，那先開個15度好了。
過了5分鐘，室溫果真快速降低，現在已經到20度，趕快把冷氣調成20度。
再過了2分鐘，ㄨㄚˊ怎麼變19度了...，那我再調成21度
過了幾分鐘，阿又變成20.5度...

當室溫與目標值差異很大的時候，我們會輸出較低的溫度(假設室溫>目標值)，而等到溫差很小，或是溫度顯示已經達目標值時，我們就輸出與目標值相當接近的溫度。
但問題來了，為什麼我們在顯示為20度時，將冷氣設為20度，溫度卻還會繼續下降呢?
一般的感測器都會有延遲的現象，像實驗室時常用的酒精溫度計，總是要放一陣子以等待溫度平衡。因此當它顯示20度時，實際上很可能室溫是小於20度的。

比例控制

事實上，上面的這個控制的思路很類似P的運算。再舉另外一個例子，假設初始時刻，水缸裡的水位是0.2米，那麼當前時刻的水位和目標水位之間是存在一個誤差的(error)，。假設旁邊站著一個人，這個人通過往缸里加水的方式來控制水位。如果單純的用比例控制演算法，就是指加入的水量u和誤差error是成正比的。
u=kperror
假設kp取0.5，現在的水位高度是0.2，目標值為1
t=1時，error=1-0.2=0.8，u=0.50.8=0.4，因此水位從0.2上升到0.6
t=2時，error=1-0.6=0.4，u=0.5*0.4=0.2，因此水位從0.6上升到0.8
如此這麼循環下去，最終水位會到達我們所設定的1。

但是，單單的比例控制存在著一些不足，其中一點就是–穩態誤差！
像上述的例子，根據kp取值不同，系統最後都會達到1米，只不過kp大，到達的快，kp小了到達的慢一些。不會有穩態誤差。但是，考慮另外一種情況，假設這個水缸在加水的過程中，存在漏水的情況，假設每次加水的過程，都會漏掉0.1米高度的水。仍然假設kp取0.5，那麼會存在著某種情況，假設經過幾次加水，水缸中的水位到0.8時，水位將不會再變換！！！因為，水位為0.8，則誤差error=0.2. 所以每次往水缸中加水的量為u=0.5*0.2=0.1.同時，每次加水，缸裡又會流出去0.1米的水！！！加入的水和流出的水相抵消，水位將不再變化！！
實際上，這種類似於「漏水」的情況相當常見，以馬達來說，摩擦力就相當於是這個例子中的「漏水」。

積分控制

還是用上面的例子，如果僅僅用比例會存在穩態誤差，最後的水位就卡在0.8了。於是，在控制中，我們再引入一個分量，該分量和誤差的積分是正比關係。所以，比例+積分控制演算法為：
u=kp*error+ ki∗∫ error
大家可能會好奇實際寫程式要怎麼做積分?又不是已經知道的一個函數。沒錯，事實上我們並不是在做積分，而是在離散情況下做累加(sigma)。

還是用上面的例子來說明，
第一次的誤差error是0.8，第二次的誤差是0.4，∫error=0.8+0.4=1.2. 這個時候的控制量，除了比例的那一部分，還有一部分就是一個係數ki乘以這個積分項。由於這個積分項會將前面若干次的誤差進行累計，所以可以很好的消除穩態誤差（假設在僅有比例項的情況下，系統卡在穩態誤差了，即上例中的0.8，由於加入了積分項的存在，會讓輸入增大，從而使得水缸的水位可以大於0.8，漸漸到達目標的1.0.）這就是積分項的作用。

微分控制

換一個另外的例子，考慮刹車情況。平穩的駕駛車輛，當發現前面有紅燈時，為了使得行車平穩，基本上提前幾十米就放鬆油門並踩刹車了。當車輛離停車線非常近的時候，則使勁踩刹車，使車輛停下來。整個過程可以看做一個加入微分的控制策略。
與積分控制類似，在離散的情況下，我們沒辦法做到真正的「微分」，我們實際上在做的是error的差值，就是t時刻和t-1時刻error的差，即u=kd*（error（t）-error（t-1））/T，其中的kd是一個係數項。可以看到，在刹車過程中，因為error是越來越小的，所以這個微分控制項一定是負數，在控制中加入一個負數項，他存在的作用就是為了防止汽車由於刹車不及時而闖過了線。
切換到上面給水缸加水的例子，就是當發現水缸裡的水快要接近1的時候，加入微分項，可以防止給水缸裡的水加到超過1米的高度，說白了就是減少控制過程中的震盪。

最後附上一個公式作為今天的結尾