Chap.III 深度學習與模型優化

Part 1：Neural Network 神經網路

即使用程式碼模擬生物神經傳導系統，教導機器如何學習人類思考模式並做出決策。

1-1. Basic 基本介紹

生物體內的神經網路運作流程：
外部刺激 → 神經元 → 中樞 → 大腦分析 → 下決策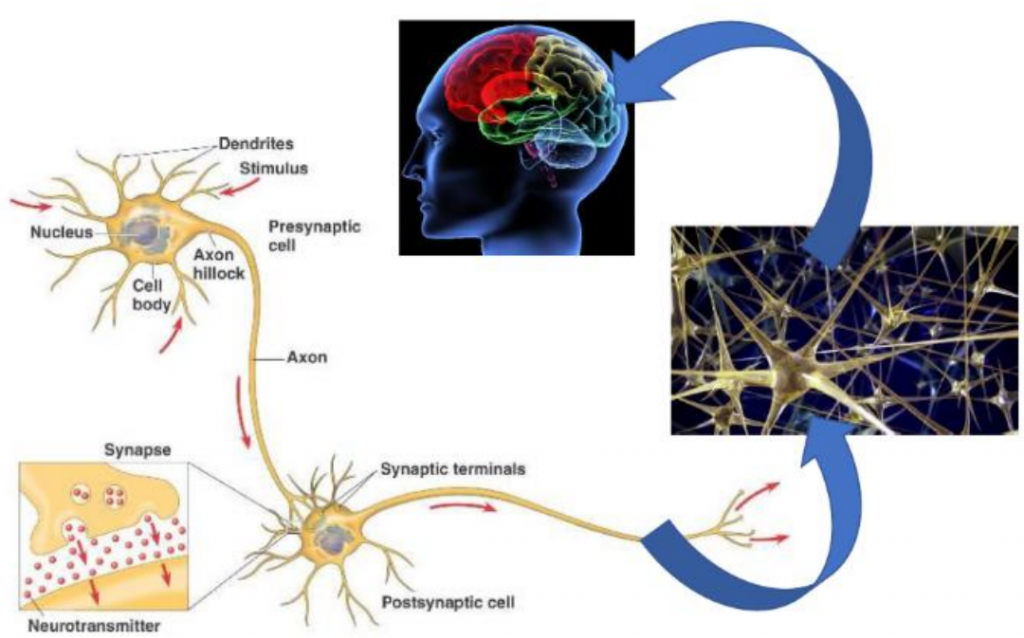

然而，實際上程式碼結構如下：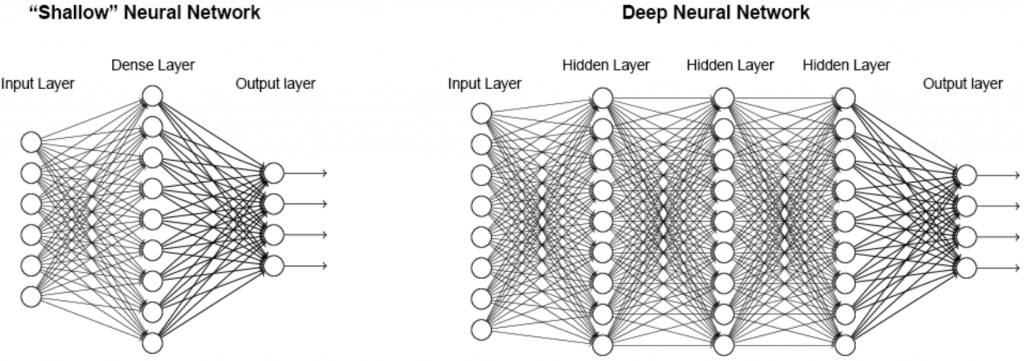

經過層層迴歸後，最終讓機器判斷結果。

1-2. Linear regression 線性迴歸

概括而論，我們訓練演算法、建立模型的過程，其實就是在求以下方程式的 w & b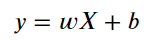

通常會用矩陣計算找出 Weight 權重與 bias 偏差值。

正向與反向傳導

1. 正向傳導：input 藉由隱藏層求得 output，計算出損失函數（MSE）的過程。
2. 反向傳導：透過優化器，不斷更新權重，最終找到最小的 MSE，的過程。
   

Loss function 損失函數

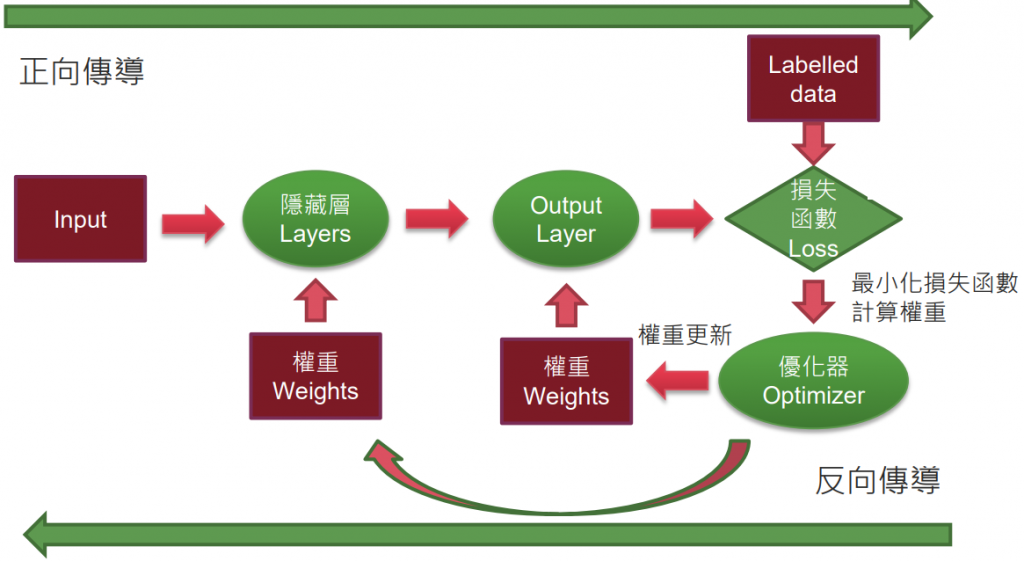
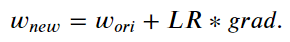
可以理解成準確度最高，損失函數就越少。故所有模型皆在力求損失函數最小化。

1. 迴歸的損失函數：Mean-Square-Error (MSE) 均方誤差

是一種評估迴歸線預測準度的指標。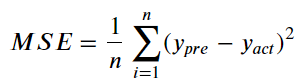

1. y_pre：模型訓練資料的預測值
2. y_act：訓練資料的實際值

2. 分類的損失函數：Cross-entropy 交叉熵

即是在Decision Tree 決策樹 有提過的 Entropy 及 information gain 概念。

Weight calculate 權重計算

1. 最小平方法（證明見補充1.）
2. 最大概似法（證明見）
   不論哪種，其結果均為：
   

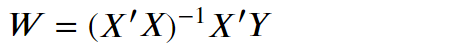
*注意：企業中使用的神經網路常具備多層，須用微分的連鎖率實現一次計算所有權重。

1-3. Activation Function 激勵函數

在深度學習中，會遇到許多「非線性」求解的問題。比如說這個漩渦的收斂：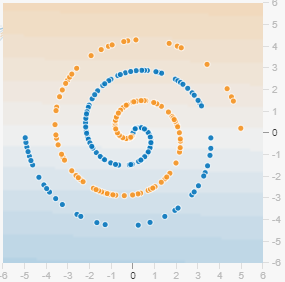

此圖明顯不是線性收斂能完成的，這時就需要 Activation function 激勵函數來轉換 output。

它的概念是：
將 x1, x2, x3...的迴歸結果 y，透過方程式 g(y) 進行轉換，進而產出全新的 output z。
我們就稱 g(z) 即是 x 的激勵函數。

常見的有以下三種：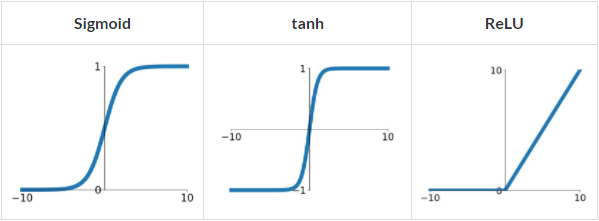

最好理解的就是 relu，即「y 大於 0 保留，y 小於 0 捨棄」，最容易計算，速度最快。
反而是 sigmoid 和 tanh 都會有梯度爆炸和梯度消失問題。

1. 沒有激勵函數的收斂情況，基本等於沒收斂：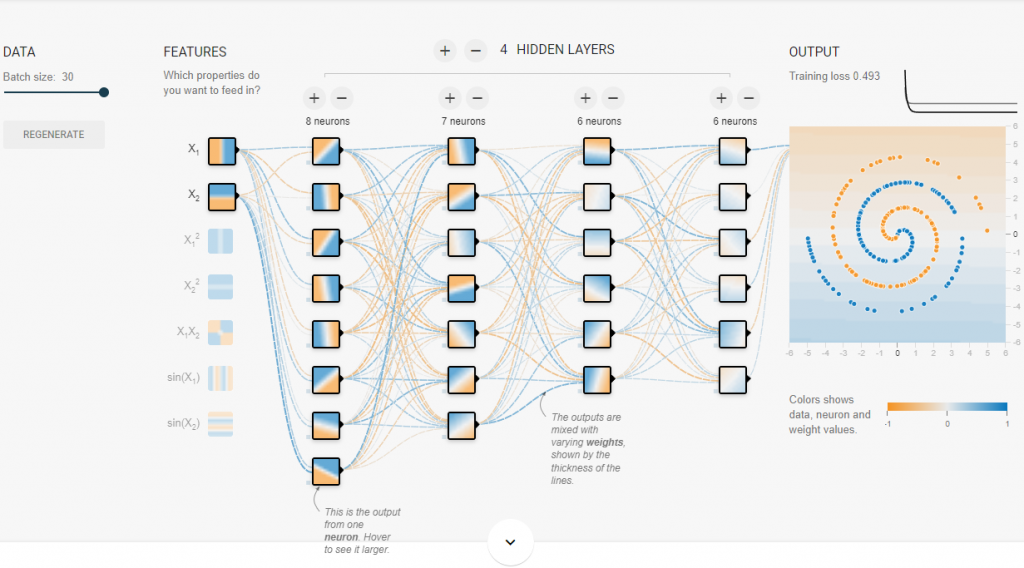
   

2. 使用 relu 激勵函數的收斂情況，約1000 Epoch 就收斂的不錯：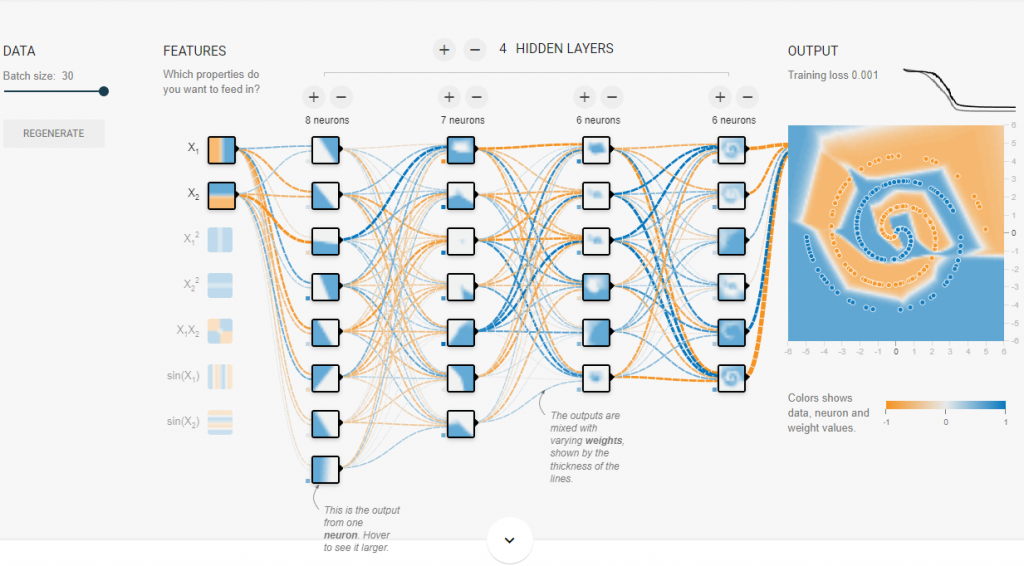
   

梯度消失 & 梯度爆炸?

在更新模型 w 時要取梯度，當然也會對激勵函數做梯度下降。
以 sigmoid 來說，對其微分後，只有在 [0-1] 的範圍內有梯度更新，其餘都是0。
所以在y > 1 or y < 0的區段是「沒有梯度的」，這就是 梯度消失。

梯度消失使後層（靠近輸出層） w 更新快，而前層（靠近輸入層）由於梯度傳遞不過去而得不到更新。
導致前層 w 幾乎不變，接近於初始化的 w。
在網絡很深的時候，學習的速度將會非常慢，甚至無法學習。

反之，若是在 [0-1] 之間梯度會持續被放大，對於一個較深的模型，
在越深的地方就會收到連續的放大倍數，梯度會變很大，此稱為梯度爆炸 。

梯度爆炸讓梯度從後往前傳時不斷增大，w 更新過大，使函數在最優點之間不斷波動。

當然，仍然有其他的激勵函數，
但目前中間層較常用的是 Relu，分類層則較常用 Softmax。

1-4. Optimizer 優化器

根據不同的演算優化器，計算效率也不同，如下圖：
（今後會較常使用的優化器叫 Adam）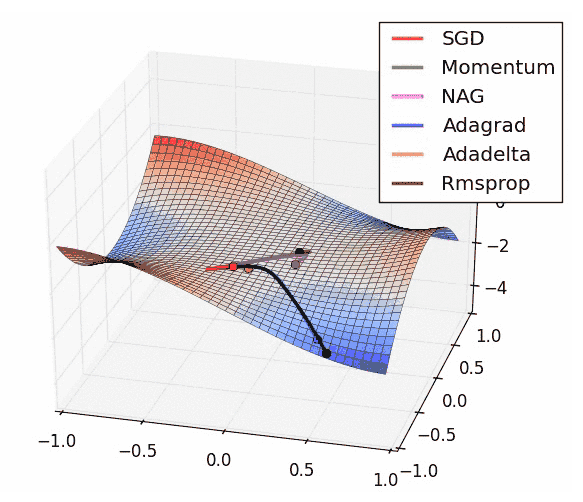

梯度下降也是一種優化方式。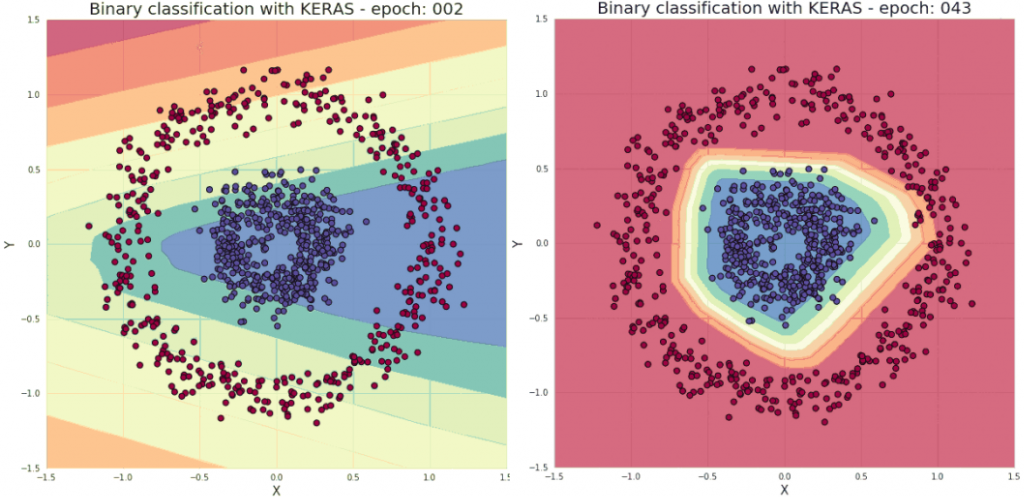

訓練過程中，準確率與損失率最終會趨近平緩。
通常來說，找到一個適合的 learning rate 是優化關鍵。
如下圖，太高的 lr 可能導致找不到最佳解，太低的 lr 則讓優化效率過低。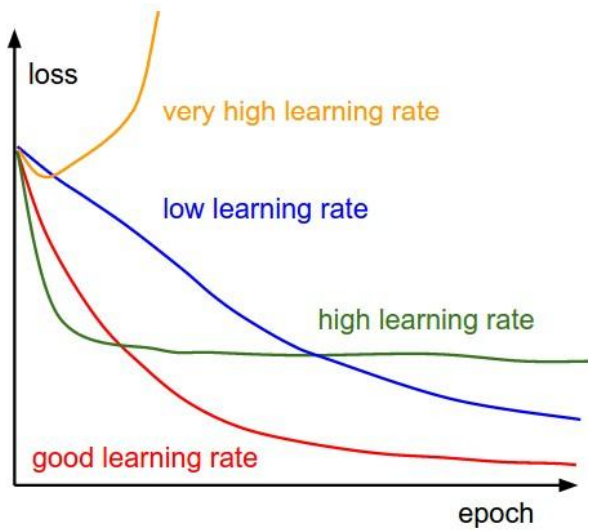

1-5. 梯度下降

首先我們必須記住以下公式：

1. Error
   
2. 梯度公式(證明見補充2.)
   
3. 權重更新
   

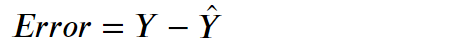
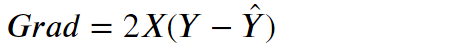
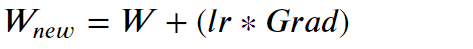
根據梯度下降的過程，又分為三種：
A. Batch Gradient Descent (BGD) 批量梯度下降法
採用「所有」樣本，作為一次 epoch。容易走到最小值，但較耗時。
B. Stochastic Gradient Descent (SGD) 隨機梯度下降法
採用「一個」樣本，作為一次 epoch。過程取決抽樣的樣本好壞，較省時。
C. Mini-batch Gradient Descent 小批量梯度下降法
採用「多個」樣本，作為一次 epoch。為上述兩者的平衡。通常也會稱為 SGD

Part 2：Deep learning framework 深度學習套件

2-1. theano：

2007 年由蒙特婁大學的蒙特婁學習算法研究所（MILA）開發，但因其本身為學術界開發且使用，在 FB、Google
等企業漸漸主導市場後，已於 2020 年 7 月起宣布不再更新版本。

2-2. Coffe/Coffe2 & PyTorch：

Coffe 是 2013 由加利福尼亞大學柏克萊分校的賈揚清開發，2017 年時 FB 發布 Coffe2，後又於 2018 宣布整
併入 PyTorch。

2-3. Keras & Tensorflow：

Keras 是 2015 由　弗朗索瓦·肖萊開發，於 2017 年由 Google 主導，將 Keras 與 Tensorflow 2.0 功能整
合後，Keras 便於 2.4v 後宣布停止更新與開發。

優勢比較：

PyTorch 語法簡潔易懂、採用動態計算圖、擁有完善的 doc，且語法設計上與 NumPy 是一致的熟悉 Python/NumPy 的深度學習初學者很容易上手。
Keras (Tensorflow 2.0) 則容易撰寫、社區支持佳，可輕鬆搭建深度學習模型。然其艱澀的語法和太底層的接口是其致命傷。
整體來說， PyTorch 適合研究（稱霸學術界），而 Tensorflow 適合產品的開發（推出較早被業界泛用）。

而此處將著重於 Tensorflow。

Part 3： Tensorflow

Tensorflow 官方網站 提供一段辨識數字的程式碼，
以下我們將逐行分析它的功能：

A. 官方網站版

import tensorflow as tf

mnist = tf.keras.datasets.mnist

(x_train, y_train),(x_test, y_test) = mnist.load_data()

model = tf.keras.models.Sequential([
  tf.keras.layers.Flatten(input_shape=(28, 28)),
  tf.keras.layers.Dense(128, activation='relu'),
  tf.keras.layers.Dropout(0.2),
  tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

model.fit(x_train, y_train, epochs=10)
model.evaluate(x_test, y_test)
>> loss: 0.0746 - accuracy: 0.9788

Tensorflow 的演算流程僅用了 10 行，且準確率達 97.8%！

B. 逐步講解版

1. Dataset

import tensorflow as tf
mnist = tf.keras.datasets.mnist

2. Clean Data
   此處不需要。

3. Split Data

(x_train, y_train),(x_test, y_test) = mnist.load_data()

*可以用矩陣畫出資料的內容物（也可用 matplotlib 畫，見補充3.）：

data_one = x_train[0].copy()   # 第一筆訓練資料取出
data_one[data_one>0]=1         # 將非 0 數據換成 1，方便辨識

for i in range(28):            # 把每一行印出來
    print(str(data_one[i]))

隱約看到數字"5"，接著對答案：

print(y_train[0])
>> 5

答案的確是"5"

3. Feture Engineering
   通常為了運算效率，會在此處多一步驟將資料常態化：

x_train_n, x_test_n = x_train / 255.0, x_test / 255.0

5. 建立 Model

model = tf.keras.models.Sequential([
  tf.keras.layers.Flatten(input_shape=(28, 28)),
  tf.keras.layers.Dense(128, activation='relu'),
  tf.keras.layers.Dropout(0.2),
  # 分類基本上都會加入一層 'softmax' 的 activation function，讓它機率和為 1
  tf.keras.layers.Dense(10, activation='softmax')
])

# 選用優化器(此處為 'adam')
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

各神經層作用如下：
5-1. Flatten Layer：扁平化。將寬、高 28*28 個像素的 2-D 圖轉成 1-D 784 個特徵。
5-2. Dense Layer：全連接層。等同添加一個 output 為 128 條迴歸線（神經元）的層。
5-3. Dropout Layer：訓練週期中，隨機拿掉部分神經元（此處為 20%)，減少對權重依賴，防止過擬合。（示意圖見補充4.)
5-4. Dense Layer：全連接層。等同添加一個 output 為 10 個神經元（對應數字0~9）的層。
經 softmax 將其轉成 0~9 的機率，以最大機率者為預測值。

6. Training Model
   若將測試資料再拆分20%作為訓練過程中的驗證：

his = model.fit(x_train_n, y_train, epochs=5, validation_split=0.2)

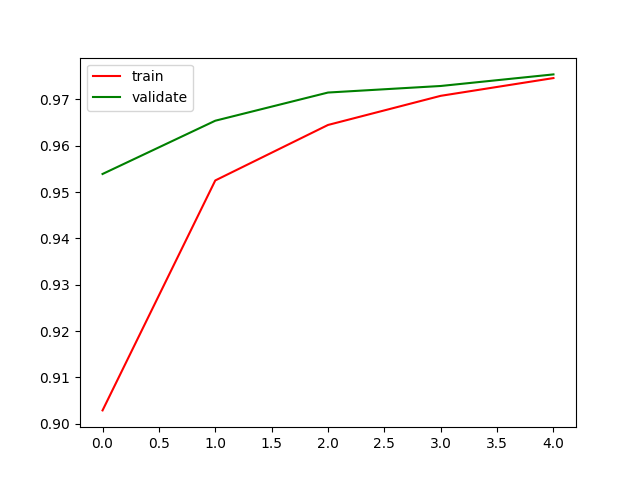
準確率與損失函數的圖畫出，兩條線應該會逐漸靠攏：

# 準確率
plt.plot(his.history['accuracy'], 'r', label='train')
plt.plot(his.history['val_accuracy'], 'c', label='validate')
plt.show()

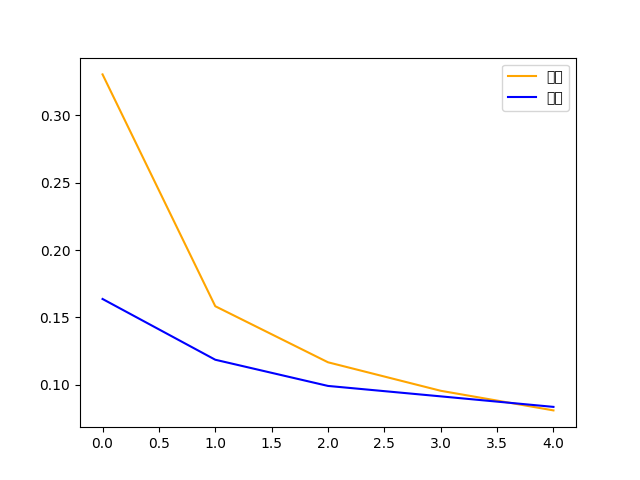
# 損失函數
plt.plot(his.history['loss'], 'm', label='train')
plt.plot(his.history['val_loss'], 'b', label='validate')
plt.show()

7. Score Model

score = model.evaluate(x_test, y_test)
print(score)
>> loss: 0.0746 - accuracy: 0.9788

8. Test Model

import numpy as np
pre = np.argmax(model.predict(x_test_n), axis=1)  # 預測資料，並且每一列取最大值(最有可能的數字)
print("Predict:", pre[0:20])
>> Predict: [7 2 1 0 4 1 4 9 6 9 0 6 9 0 1 5 9 7 3 4]
print("Actual:", y_test[0:20])
>> Actual: [7 2 1 0 4 1 4 9 5 9 0 6 9 0 1 5 9 7 3 4]

此時發現第八筆資料有錯誤，將其預測值機率調出：

pre_prob = model.predict(x_test_n)
np.around(pre_prob[8], 1)
>> array([0. , 0. , 0. , 0. , 0.2, 0.1, 0.7, 0. , 0. , 0. ], dtype=float32)

發現預測機率最高的確是數字"6"，只好調出真實圖片：

X_8 = x_test_n[8,:,:]
plt.imshow(X_8.reshape(28,28), cmap='gray')
plt.axis('off')
plt.show()

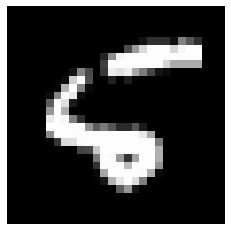
......確實長得很醜XD

9. Save Model
   最後當然是把這個模型存起來，下次調用時就不用重新建模。

model.save('Model_NumberReg.h5')

10. Reload & Testing Model
    我們用小畫家隨意地畫出一個數字：
    
    接著叫出訓練好的模型，對它做預測：

model = tf.keras.models.load_model('Model_NumberReg.h5')

# 輸入圖檔
uploaded = './myDigits/9.png'
image1 = io.imread(uploaded, as_gray=True)

# 壓縮圖檔畫素
image_resize = resize(image1, (28, 28), anti_aliasing=True)
X1 = image_resize.reshape(1, 28, 28)

# 反轉顏色（顏色 0 為白，RGB (0, 0, 0) 為黑）
X1 = np.abs(1-X1)

# 使用 Model 預測
pre = np.argmax(model.predict(X1))
print(pre)
>> 9

這樣就完成了 Tensorflow 的機器學習初體驗啦~

*後續思考：

1. 最後一層參數總數算法?（GPT-3 已經高達 1750 億個參數!）
2. Dense 的參數?
3. Activate function 要選用哪個?
4. Ragularization 的作用?
5. Dropout 是甚麼? 該擺放在哪一層? 比例又該如何選擇?
6. 損失函數有哪些? 個別有甚麼影響?
.
.
.
.
.
*補充1.：最小平方法

為了求得 SSE（沒有除以 n 項的 MSE）最小化，我們首先要定義 Error：

矩陣內容如下：

因為要讓 E 為正值，將其平方：

（此處 Y'X\beta 與 \beta'X'Y 因為皆為常數且值相等，故簡化成一項次）

為了求得 SSE 最小，將其對 \beta' 微分求導，且結果為 0：

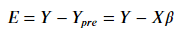
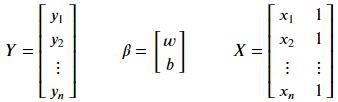
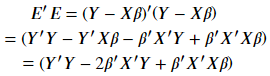
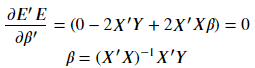
*補充2.：梯度公式

SSE 的定義如下：

其中 y_i 表示預測值；\hat{y_i} 表示平均值，而因為 y_i = (wx_i + b)

而梯度的定義為下：

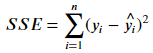
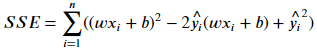
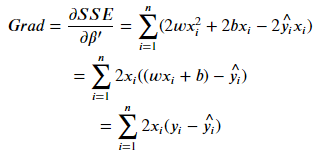
*補充3.：用 matplotlib 畫出資料的內容物

# 
import matplotlib.pyplot as plt
data_one = x_train[0]
plt.imshow(data_one.reshape(28, 28), cmap='gray')
plt.axis('off')
plt.show()

*補充4.：Dropout Layer 示意圖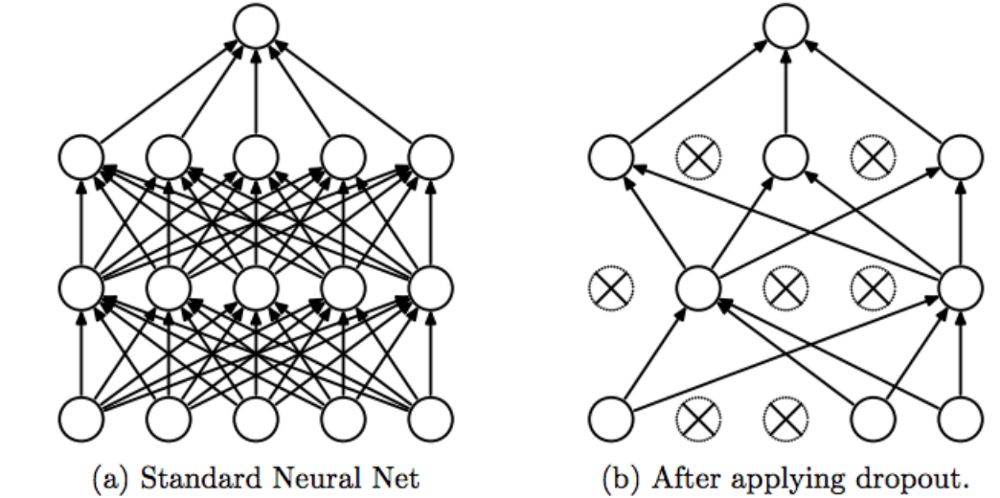

.
.
.
.
.

Homework：

請使用網站的資料（日文辨識），作為機器學習的對象。