前言

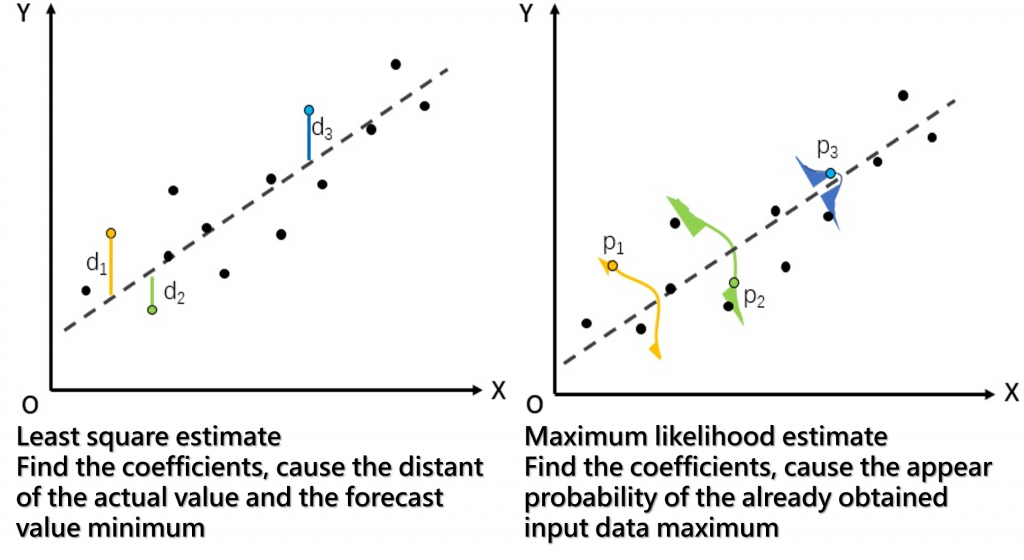
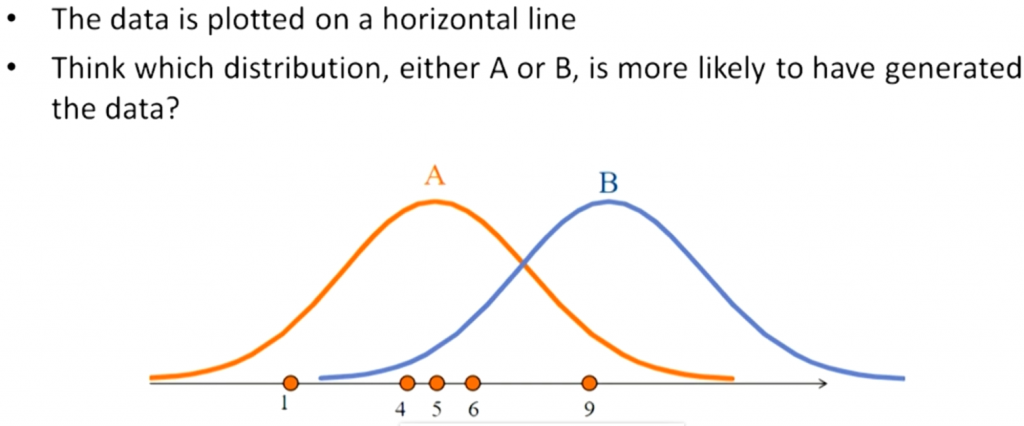
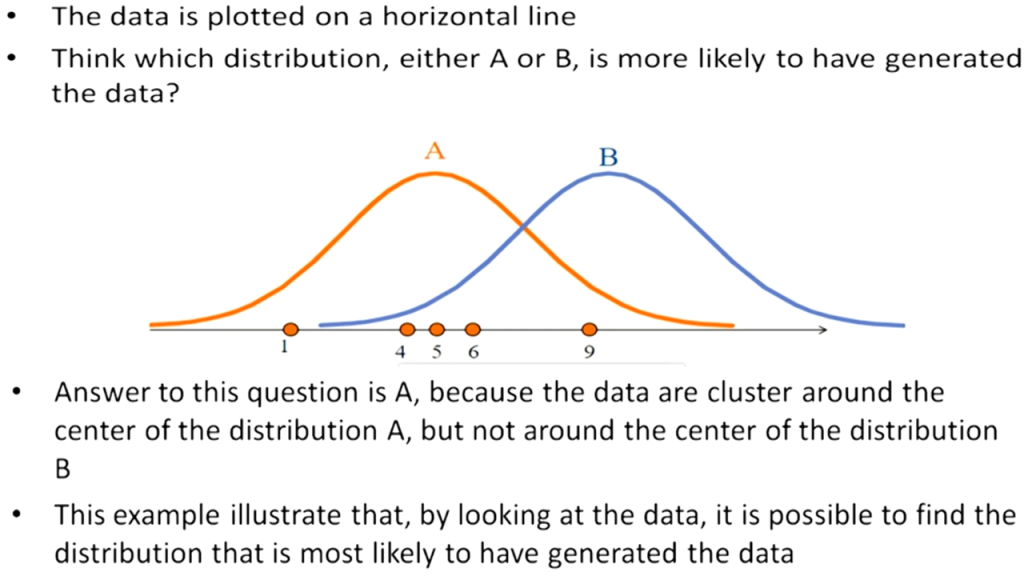
【上一篇】介紹了最小平方法(OLS)，接下來，就來欣賞一下『最大概似法』(Maximum likelihood estimation, MLE)，它是另一種估算參數值的方法，同樣的，筆者會以圖表的方式說明，讓大家輕鬆地領略MLE的美妙之處。

其中，涉及數學證明，希望能以淺顯的角度說明，如不夠精準，還請不吝指正。

問題說明

同樣是線性迴歸的問題，如下圖，我們希望找到迴歸線的參數 -- 斜率(W)及偏差(b)，上一篇求解的關鍵點是我們訂定目標函數為『極小化誤差』，在此前提下，以『最小平方法』(OLS) 可以找到了一組參數值，能達成目標: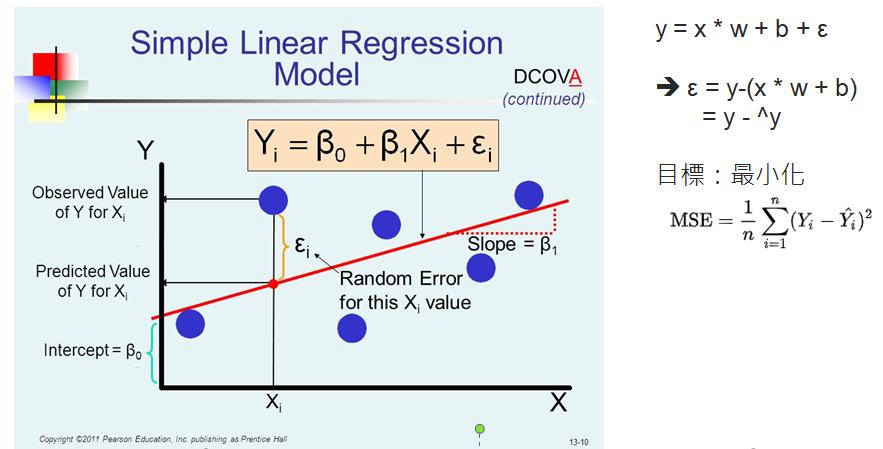

圖片來源：tirthajyoti/Machine-Learning-with-Python

『最大概似法』(MLE) 它的出發點與『最小平方法』不一樣，顧名思義，假設有三條迴歸線如下圖，MLE要找出有『最大可能』代表樣本的一條線。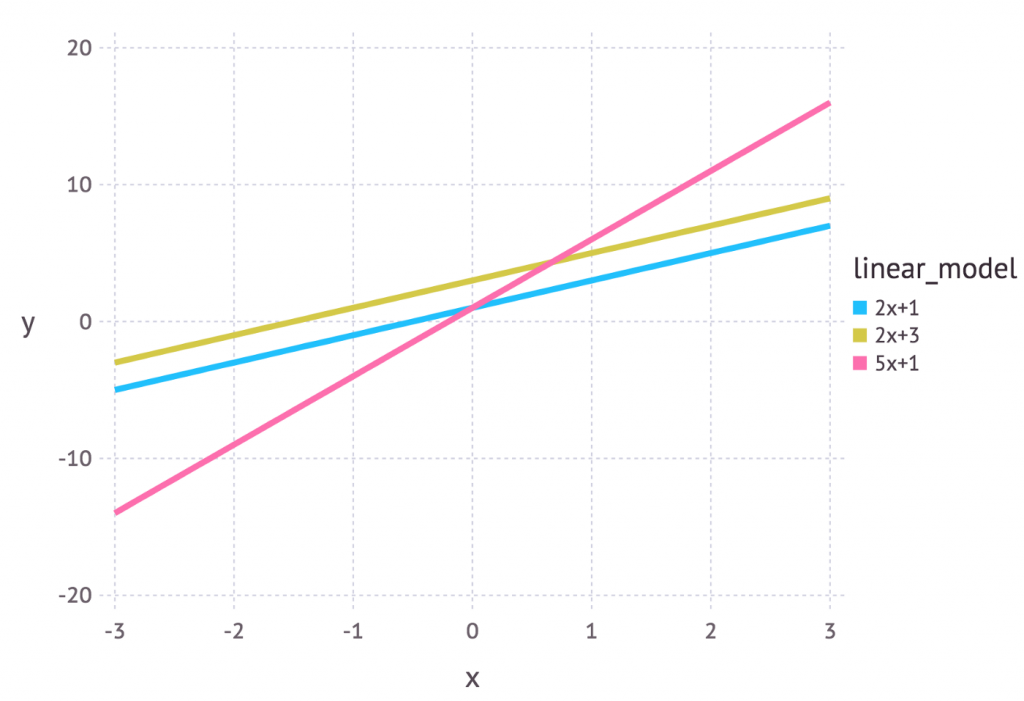

圖片來源：Probability concepts explained: Maximum likelihood estimation

又例如另一個問題，如下圖，有一堆樣本點(淺藍色的圓點)，它們『最大可能』是來自哪一種常態分配(f1、f2、f3或f4)。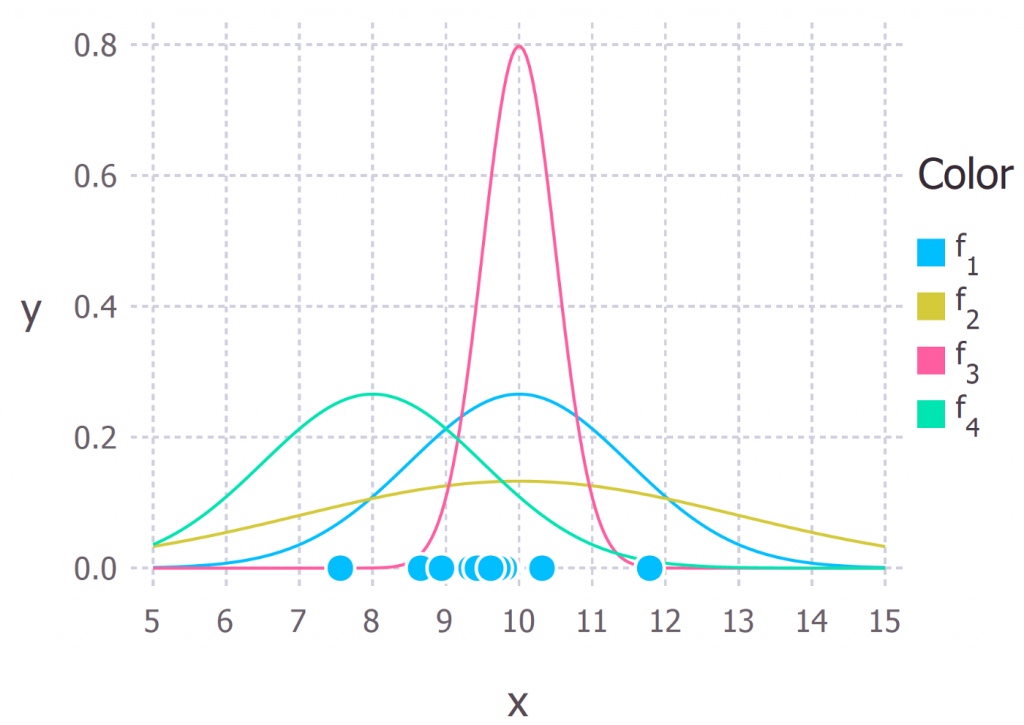

圖片來源：Probability concepts explained: Maximum likelihood estimation

下面就來看看，以上題為例，MLE如何估算參數值。
首先介紹『常態分配』(Noraml Distribution)的機率分配函數如下：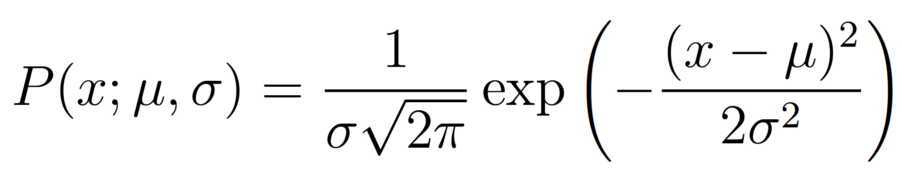

假設所有樣本來自同一常態分配，且樣本之間是相互獨立的，這很重要，如果樣本違反假設，以下的推論就是錯的。

假設有三筆觀察值，分別為 9, 9.5, 11，因為樣本之間相互獨立，故聯合機率(joint probability)公式如下：

P(A∩B∩C) = P(A) x P(B) x P(C)

計算如下：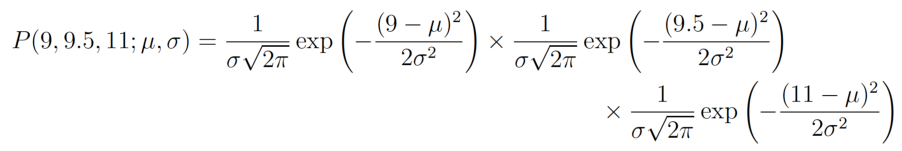

通常有指數不好算，所以，等式兩邊各取log(兩個數字經過Log運算，大者恆大，以此類推，故聯合機率加log後，最大值時的參數值估算還是不變)：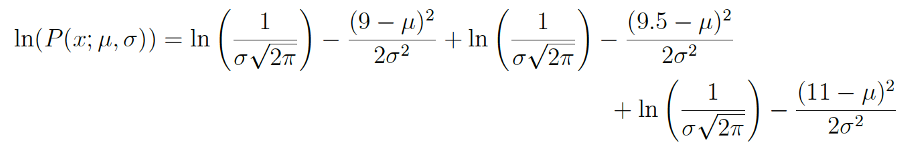

帶入樣本值，得到：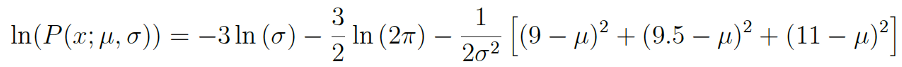

對μ偏微分，一階導數=0時有最大值，估算出參數μ=9.833：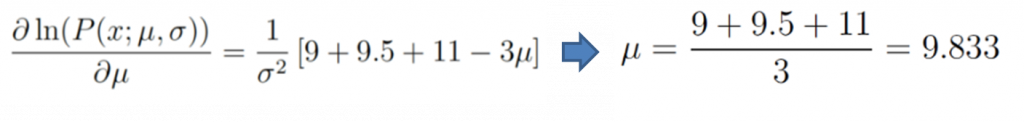

同樣對標準差(σ)偏微分，就可估算出參數值σ。

線性迴歸模型求解

y = βx + ξ

其中誤差(ξ) 即符合假設『所有樣本來自同一常態分配，且樣本之間是相互獨立的』，因此，

另一種應用 -- 集群(Clustering)

高斯混合模型(Gaussian mixture model, GMM)，就是利用MLE，去推估每個樣本最有可能屬於某一常態分配，藉此達到分群(Clustering)的效果，如下圖。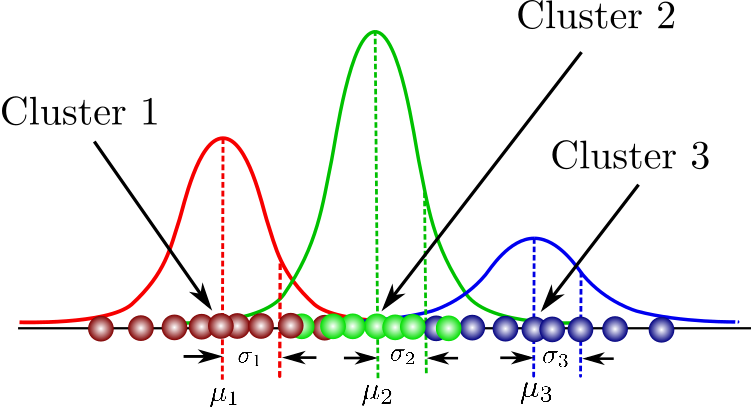

圖片來源：Gaussian Mixture Models Explained

結論

有人說『最小平方法』是『最大概似法(MLE)』的一種特例，最大概似法(MLE)有更多的場景可以應用，你認為呢 ?