Chap.III 深度學習與模型優化

Part 3： Tensorflow - 續

上一篇章簡介了 tensorflow 的程式碼，同時也留下了幾個後續思考的問題。
這邊就以同樣是 mnist 的資料集 fashion 來展開討論。

# Datasets
import tensorflow as tf
mnist = tf.keras.datasets.fashion_mnist
(x_train, y_train),(x_test, y_test) = mnist.load_data()

# Feature Engineering
x_train_n, x_test_n = x_train / 255.0, x_test / 255.0

# Model
model = tf.keras.models.Sequential([
    tf.keras.layers.Flatten(input_shape=(28, 28)),
    tf.keras.layers.Dense(128, activation='relu'),
    tf.keras.layers.Dropout(0.2),
    tf.keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# Training model
his = model.fit(x_train_n, y_train, epochs=5, validation_split=0.2, steps_per_epoch=800)

# Score model
score = model.evaluate(x_test, y_test)
score

>>  [54.680458068847656, 0.8521999716758728]

1. 最後一層參數總數算法?

我們可以透過 mdoel_load.summary() 指令來獲得參數量。

mdoel.summary()

>>  Model: "sequential_1"
    _________________________________________________________________
    Layer (type)                 Output Shape              Param #   
    =================================================================
    flatten_1 (Flatten)          (None, 784)               0         
    _________________________________________________________________
    dense_2 (Dense)              (None, 128)               100480    
    _________________________________________________________________
    dropout_1 (Dropout)          (None, 128)               0         
    _________________________________________________________________
    dense_3 (Dense)              (None, 10)                1290      
    =================================================================
    Total params: 101,770
    Trainable params: 101,770
    Non-trainable params: 0
    _________________________________________________________________

為什麼是 1290?

最後一層的 input 是 128 個權重，那麼我們可以把其一的迴歸線寫作：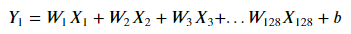

總共有 128 個權重 W 與 1 個偏差項 b，共 129 個參數。
再來， output 共輸出了 10 條迴歸線，故總參數量就是 129*10 = 1290!

以 GPT-3（一種自迴歸語言模型）來說，含有高達 1750 億個參數呢!

2. 哪些品項容易混淆?

要查看哪些品項容易誤判，這時候我們就可利用先前說過的混淆矩陣來幫忙了。

# 如何畫出「好看的」混淆矩陣
import sklearn.metrics as skm
import numpy as np
pre = np.argmax(mdoel_load.predict(x_test_n), axis=1)  # 預測資料，並且每一列取最大值(最有可能)

cm = skm.confusion_matrix(y_true=y_test, y_pred=pre)

# 用 seaborn 畫
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(10, 6))
labels=np.arange(10)
sns.heatmap(
    cm, xticklabels=labels, yticklabels=labels,
    annot=True, linewidths=0.1, fmt='d', cmap='YlGnBu')
plt.title('Confusion Matrix', fontsize=15)
plt.ylabel('Actual label')
plt.xlabel('Predict label')

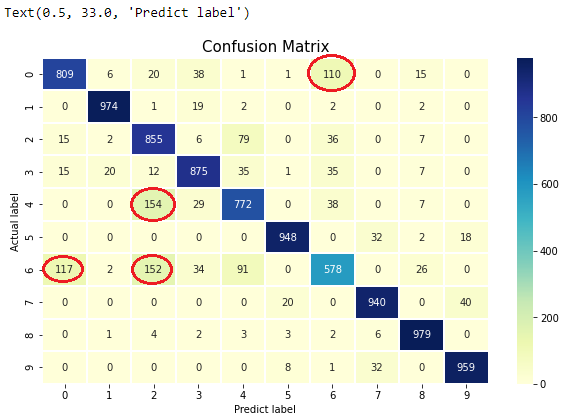
這樣一來，很清楚可以看到

1. 有 110 個品項 0（T-shirt）被預測成 品項 6（Shirt）
2. 有 154 個品項 4（Coat）被預測成 品項 2（Trouser）
3. 有 117 個品項 6（Shirt）被預測成 品項 0（T-shirt）
4. 有 152 個品項 6（Shirt）被預測成 品項 2（Pullover）

看來衣服真的很容易預測錯誤呢(笑)

3. Dense 的參數?

我們可以參考Keras 官網：

1. units: 正整數，輸出空間維度。
2. activation: 激勵函數。若不指定，則不使用激活函數 (即「線性」: a(x) = x)。
3. use_bias: 偏差項。即 y=wx + b 中的 b。
4. initializers
   4-1. kernel_initializer: w 的初始化器。
   4-2. bias_initializer: b 的初始化器。
5. regularizers https://keras.io/zh/regularizers/
   5-1. kernel_regularizer: w 的正則化函數。
   5-2. bias_regularizer: b 的正則化函數。
6. activity_regularizer: 正則化函數。
7. constraint
   7-1. kernel_constraint: 限制 w 的範圍。
   7-2. bias_constraint: 限制 b 的範圍。

4. Activate function 要選用哪個?

在前篇我們已經有討論過，依照現有的研究指出，ReLU（可接受 0）及 LeakyReLU（不可接受 0）在大部分情況下效果會最好。
其他還有像是早期使用的 Sigmoid、tanh，以及專門用來歸一化的 softmax...等。

更多激勵函數可參考維基百科

5. Ragularization 的作用?

比起以往的演算法，神經網路特徵更多，以數字辨識為例，就有 28*28 = 784 個特徵。
過多的特徵將導致 overfitting 的問題，因此會在神經層中加入 penalty 懲罰項，以簡化 Loss function。
讓新的損失函數會變成如下: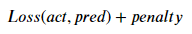

其中，我們最常使用的就是 L1 penalty & L2 penalty。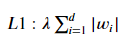

數學上來看，L1 就是直接刪去較高的權重，只針對較小的權重尋找最小的損失函數。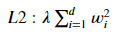

而不同於 L1，L2 不使任何權重歸零，但會將所有的權重調整，以達到簡化模型的目的。

6. Dropout 是甚麼? 該擺放在哪一層? 比例又該如何選擇?

Dropout 層就是隨機將特定比例的資料拋棄，以達到矯正 overfitting 簡化模型的目的。
基本上可以將每一層 Dense 後方都設定一層 Dropout 層。
至於 Dropout 的比例如何拿捏...那就是黑箱科學的部分了 XD！
要根據經驗，資料類型及屬性等去判斷，並沒有一定的比例是最好的～

7. 損失函數有哪些? 個別有甚麼影響?

可以參考Keras 官網中其他的損失函數。
我們目前有接觸到的兩樣如下：

1. MSE
2. Cross Entropy

然而，直接將上面的程式碼直接改成 MSE 會發現：

# Model
model = tf.keras.models.Sequential([
    tf.keras.layers.Flatten(input_shape=(28, 28)),
    tf.keras.layers.Dense(128, activation='relu'),
    tf.keras.layers.Dropout(0.2),
    tf.keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',
              loss='mse',
              metrics=['accuracy'])

# Training model
his = model.fit(x_train_n, y_train, epochs=5, validation_split=0.2, steps_per_epoch=800)

# Score model
score = model.evaluate(x_test, y_test)
score

>>  [27.61042594909668, 0.10019999742507935]

居然結果只有 10% 準確率，這是怎麼回事?

其實，這是因原本損失函數 "sparse_categorical_crossentropy" 裡，偷偷包含了一個 sparse categorical。
這個所謂的「稀疏分類」，其實就是我們熟知的「One-hot encoding」。

簡單地說，若分類結果有 10 種，他會將 y 自動拆分成 10 個欄位，
若某一樣的預測結果是「9」，那麼在「0~8」欄位裡面都會是 False，而第 9 欄位是 True。

然而 MSE 的損失函數運算並沒有這個功能，因此我們必須手動作業：

# Datasets
import tensorflow as tf
mnist = tf.keras.datasets.fashion_mnist
(x_train, y_train),(x_test, y_test) = mnist.load_data()

x_train_n, x_test_n = x_train / 255.0, x_test / 255.0

# One-hot encoding
y_train = tf.keras.utils.to_categorical(y_train)
y_train[0:1]

>>  array([9], dtype=uint8)

查看一下是不是有成功

y_train[0:1]

>>  array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]], dtype=float32)

接著 Training，就可以發現準確率回到了原先的 87% 囉！

*註記: One-hot encoding 又分 Ordinal（有序，有大小順序之分）與 Nominal（名目，僅有 True/False 之分）
.
.
.
.
.

Homework Answer：

請使用以下網站的資料（日文辨識），作為機器學習的對象。

https://github.com/rois-codh/kmnist

將四個檔案下載完成後，機器學習程式碼如下：

1. Dataset
   註：.npz檔: numpy 提供的壓縮檔模式。

import numpy as np

filename = './k49-train-imgs.npz'
arr = np.load(filename)
X_train = arr['arr_0']

filename = './k49-test-imgs.npz'
arr = np.load(filename)
X_test = arr['arr_0']

filename = './k49-train-labels.npz'
arr = np.load(filename)
y_train = arr['arr_0']

filename = './k49-test-labels.npz'
arr = np.load(filename)
y_test = arr['arr_0']

X_train.shape, X_test.shape, y_train.shape, y_test.shape
>> ((232365, 28, 28), (38547, 28, 28), (232365,), (38547,))

*隨意取出一筆資料圖片：

import matplotlib.pyplot as plt
data_one = X_train[1]
plt.imshow(data_one.reshape(28, 28), cmap='gray')
plt.axis('off')
plt.savefig('tf Japan 01')
plt.show()

看起來是日文字"と(To)"

3. Feture Engineering 常態化

X_train_n, X_test_n = X_train / 255.0, X_test / 255.0

5. 建立 Model
   要注意的是，在最後一層 Dense 全連接層須將 output 數量改為 49。

model = tf.keras.models.Sequential([
  tf.keras.layers.Flatten(input_shape=(28, 28)),
  tf.keras.layers.Dense(128, activation='relu'),
  tf.keras.layers.Dropout(0.2),
  tf.keras.layers.Dense(49, activation='softmax')
])
# 選用優化器(此處選擇 'adam')
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

6. 訓練 Model
   依然用 validation_split 把訓練資料拆出 20%，作訓練過程中的驗證

model.fit(X_train_n, y_train, epochs=5, validation_split=0.2)

7. Score Model

score = model.evaluate(X_test_n, y_test)
print(score)
>> [0.9463422894477844, 0.7574648857116699]

8. Use Model predict
   取用測試資料進行測試，取出前 20 筆對答案。

import numpy as np
pre = np.argmax(model.predict(X_test_n), axis=1)  # 預測資料，每一列取最大值(最有可能的數字)
print("Predict:", pre[0:20])
print("Actual:", y_test[0:20])

>>  Predict: [19  4 10  3 26 12 25  9 24  8 19  5 12 46 28  4  9 10  7 13]
    Actual: [19 23 10 31 26 12 24  9 24  8 19  5 12 46 28  4  9 10 18 13]

調出第 4 筆錯誤圖片

X_3 = X_test_n[3,:,:]
plt.imshow(X_3.reshape(28,28), cmap='gray')
plt.axis('off')
plt.savefig('tf Japan test 03')
plt.show()

預測為"え(E)"，實際上是"み(Mi)"

結論：看來預測文字的精準度遠遠不及預測數字呢...