昨天我們提到了資料結構跟演算法的定義及他們之間的關係，我們也可以知道，對於同一個問題，我們可以使用很多不同種類的演算法來解決他，但要怎麼判斷哪種演算法比較好呢?

這時候，我們可以用兩種判斷標準來評斷這些演算法對於這個問題的優劣:

• 時間複雜度(Time Complexity):執行演算法所需要耗費的時間成本
• 空間複雜度 (Space Complexity):執行演算法所需要耗費的空間成本，也就是所占用的記憶體空間

時間複雜度(Time Complexity)

雖然我們說時間複雜度是執行演算法所需要耗費的時間成本，但因為電腦執行的速度很快，而且不同電腦的規格不一樣，所以如果是用計算電腦跑這個演算法需要花幾分幾秒，既難計算也有失公平，所以我們主要的概念是計算**「演算法執行需要幾個指令」**

漸進式符號(Asymptotic Notations)

要計算演算法的時間複雜度我們會需要用到漸進式符號٩(｡・ω・｡)و

目的:表現時間函數的growth rate(成長速率之等級)，也就是看在input size變大的時候，執行時間以何種趨勢成長，幫助我們得知各個演算法的Complexity(複雜度)，便能決定哪個演算法較有效率。

常見的Asymptotic Notations

1. Big O：O
   f(n) = O(g(n)): ∃c、n0>0 ， such that f(n)≤c⋅g(n) ∀n>n0
   也稱g(n)為f(n)之asymptotic upper bound

2. Big Omega：Ω
   f(n) = Ω(g(n)): ∃c、n0>0 ， such that f(n)≥c⋅g(n) ∀n>n0
   也稱g(n)為f(n)之asymptotic lower bound

3. Big Theta:Θ
   f(n)=Θ(g(n)): ∃c1、c2、n0>0 ，such that c1⋅g(n)≤f(n)≤c2⋅g(n)
   也稱g(n)為f(n)之asymptotic tight bound

4. Little–o:o (絕對小於)
   f(n) = o(g(n)): ∃c、n0>0 ， such that f(n)< c⋅g(n) ∀n>n0

5. Little–Omega:ω (絕對大於)
   f(n) = ω(g(n)): ∃c、n0>0 ， such that f(n)> c⋅g(n) ∀n>n0

∃:存在
∀:for all

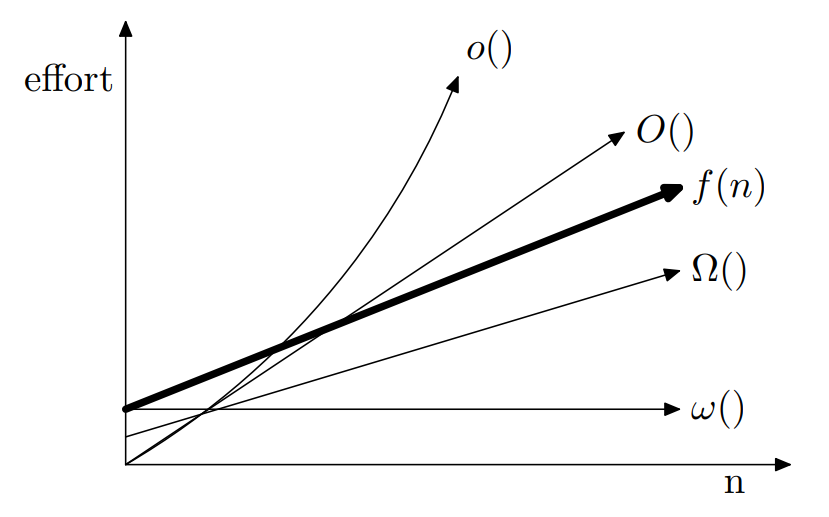
圖片來源:https://www2.cs.arizona.edu/classes/cs345/summer14/files/bigO.pdf

相關性質

1. Trainsitive(遞移性)
f(n)=Θ(g(n)) and g(n)=Θ(h(n))，則f(n)=Θ(h(n))
五個Asymptotic Notations皆滿足此特性

2. Reflexsive(反身性)
f(n) = O(f(n))
f(n) = Ω(f(n))
f(n)=Θ(f(n))
Little–o及ω不滿足此特性，因為沒有**=**

3. Symmetric(對稱性)
f(n)=Θ(g(n)) iff g(n)=Θ(f(n))
其他四個Asymptotic Notations皆不滿足此特性

常見的成長速率等級

O(1)：常數時間，演算法執行時間與輸入的資料量沒有關聯，不論n為多少都只執行常數次。
O(logn)：執行時間隨資料量呈對數比例成長，比如n輸入16，log16=4(因為2⁴=16)，所以經過4個步驟可以完成這個計算，常見的例子是二分搜尋法（Binary search）。
O(n)：執行時間隨資料量呈線性成長，像是迴圈，當輸入的n越大，執行的次數也會等比增加。
O(nlogn)：執行時間隨資料量呈線性對數成長，像是合併排序法（Mergesort）、快速排序法(Quick Sort)。
O(n²)：執行時間隨資料量呈平方成長，像是雙層迴圈、氣泡排序法（Bubble sort）。
O(n³)：執行時間隨資料量呈立方成長。
O(cⁿ)：執行時間隨資料量呈指數成長。
O(n!)：執行時間隨資料量呈階乘成長，大部分情況下，算是效率很差的複雜度。

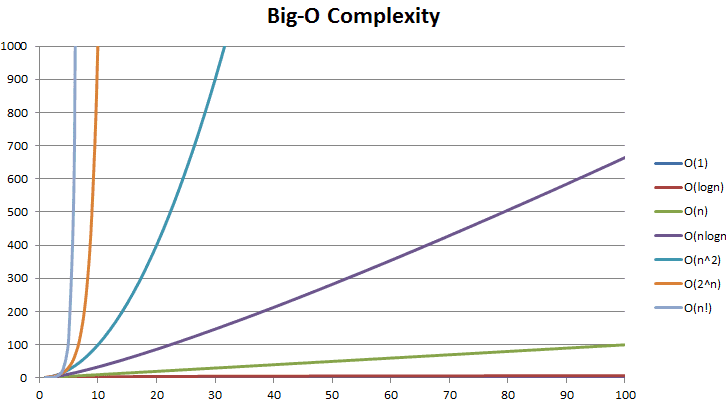
圖片來源:https://smootok.com/big-o-notation/

參考資料
Complexity：Asymptotic Notation(漸進符號)
程式人生-演算法分析
從0開始啃Introduction of algorithms心得與記錄
Asymptotic Notation