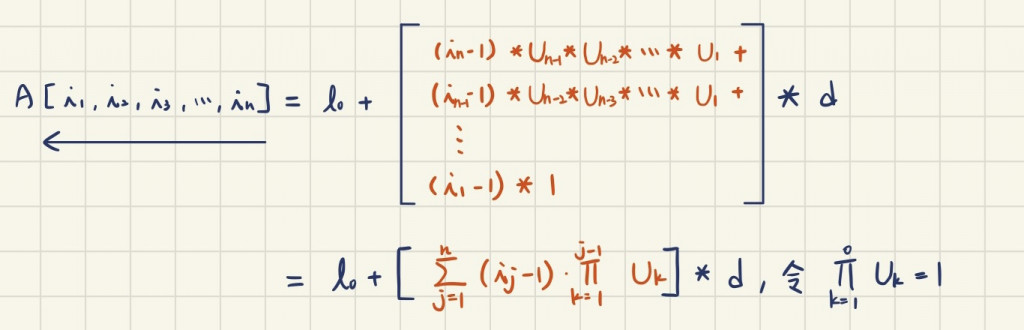陣列是什麼

陣列屬於一種靜態的資料結構，而且他會具有以下幾種特性:

1. 需要使用一段連續的記憶體空間來儲存
2. 用來儲存一群相同類型的資料
3. 可以透過索引值快速存取想要的資料
4. 需要事先宣告固定的記憶體空間，因此容易造成記憶體浪費
5. 在新增或刪除資料時，需要移動大量的資料

陣列其實像學校裡的置物櫃一樣，每個櫃子都有編好也都讓大家放置自己的物品，要找的時候只要依照外面的編號就可以快速找到｡:.ﾟヽ(*´∀`)ﾉﾟ.:｡

array的宣告方式

array宣告時通常以arraytype arrayname[position number]的方式呈現
而array若沒特別指定他的初始索引值是從0開始哦!!
也就是第一格為A[0]這樣的概念 (＊゜ー゜)b

一維陣列

資料結構

[宣告方法一] :
A:array[1..n] of item
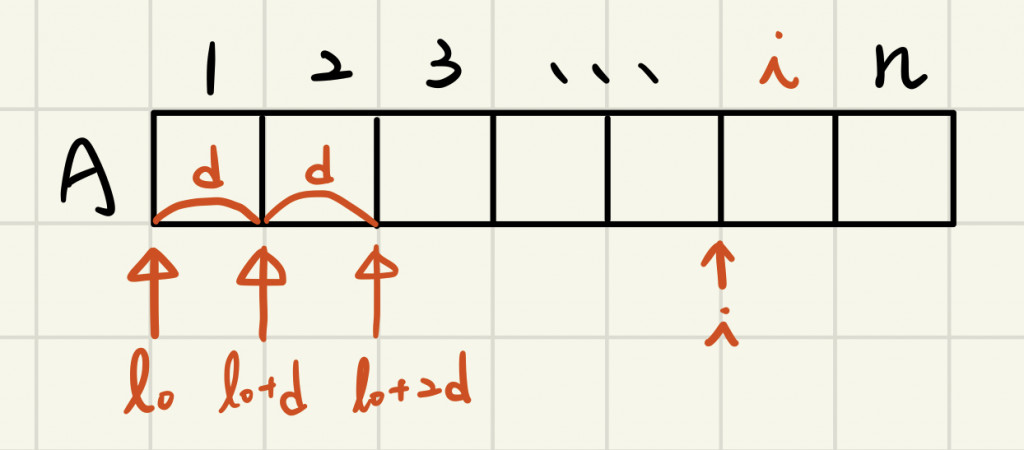
起始位址=l₀
元素大小=d
則要計算A[i]之位置(location)的公式為:l₀+(i-1)*d

是不是覺得很眼熟哇 這其實跟我們小時候學的等差公式一樣歐٩(๑•̀ω•́๑)۶

[宣告方法二] :
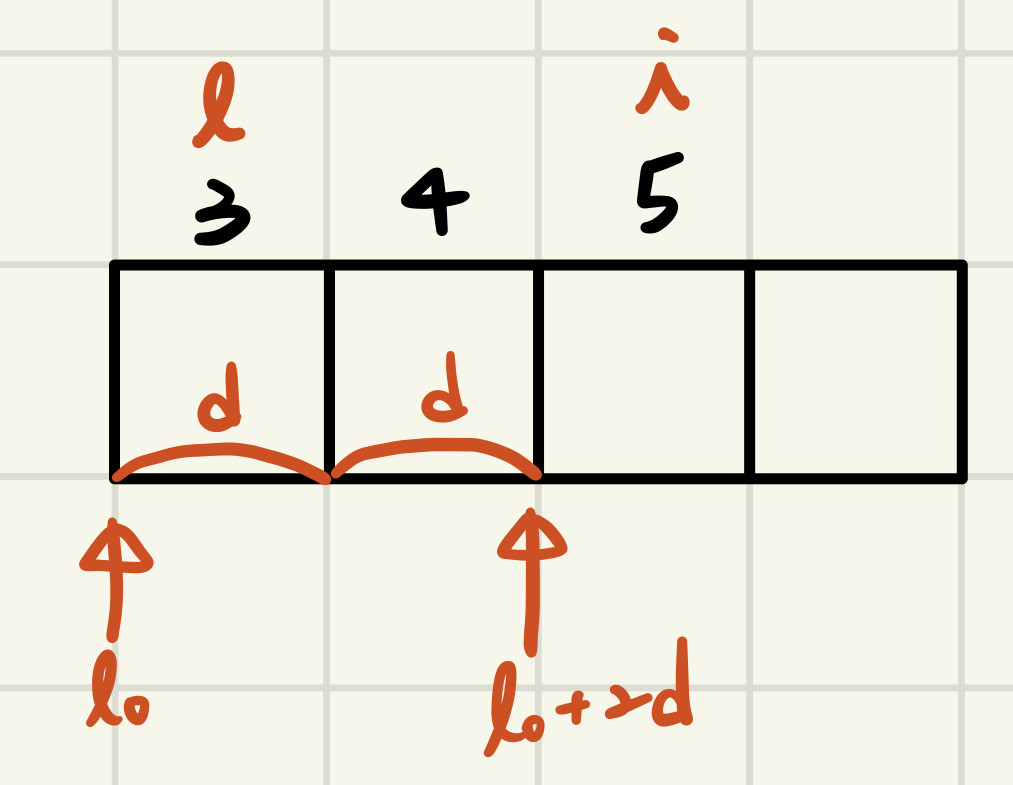
A:array[l..u] of item 有u-l+1格
則A[i]之location = l₀+(i-l)*d

C++實作

#include <iostream>
using namespace std;

int main(){
	int arraysize=10; //我們令這個陣列大小為10格
	int A[arraysize]; //宣告此一維陣列
	
	for(int i=0;i<arraysize;i++){
		A[i]=2+2*i;
		cout<<i<<":"<<A[i]<<endl;
	}
	
}

這樣我們就輕鬆製作出一個首項為2公差為2的陣列了(ﾉ◕ヮ◕)ﾉ*:･ﾟ✧
做出來的解果: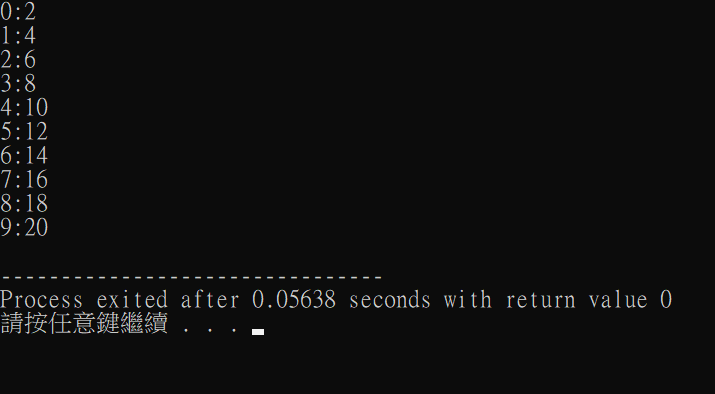

二維陣列

資料結構

[宣告方法一] :
A:array[1..m,1..n] of item
此為m列(Row)，**n行(column)**之陣列
二維陣列在記憶體中的儲存方式有:

1. Row major
   A[i,j]=l₀+[(i-1)*n+(j-1)]*d

2. Column major
   A[i,j]=l₀+[(j-1)*m+(i-1)]*d

[宣告方法二] :
A:array[l₁..u₁,l₂..u₂] of item
此陣列有**(u₁-l₁+1)列(Row)，(u₂-l₂+1)行(column)**
二維陣列在記憶體中的儲存方式有:

1. Row major
   A[i,j]=l₀+[(i-l₁)*(u₂-l₂+1)+(j-l₂)]*d

2. Column major
   A[i,j]=l₀+[(j-l₂)*(u₁-l₁+1)+(i-l₁)]*d

C++實作

#include <iostream>
using namespace std;

int main(){
//Two dimension array:arraytype arrayname [Row][Column]
	int arraysize=4;
	int a[arraysize][arraysize];
	int number=1;
	
	//row major
	for(int i=0;i<arraysize;i++){
		for(int j=0;j<arraysize;j++){
			a[i][j]=number;
			number++;
			cout<<a[i][j]<<"\t";
		}cout<<endl;
	}cout<<endl;
	
	//column major
	int row=4;
	int column=4;
	int b[row][column];
	int num=1;
	for(int m=0;m<row;m++){
		for(int n=0;n<column;n++){
			b[m][n]=m+n*row+1;
			cout<<b[m][n]<<"\t";
		}
		cout<<endl;
	}
}

我們建立一個4*4的方陣來儲存1~16這些數字
以row major的方式儲存: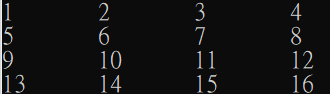

以column major的方式儲存: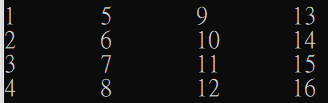

三維,四維,...,N維矩陣(要幾維就幾維喇ฅ(๑д๑)ฅ!!)

只要是≥2維，他元素的儲存方式都有兩種:

• Row major:由左而右
• Column major:由右而左

A[1..u₁,1..u₂,1..u₃] of item 三維陣列
已知l₀,d
求A[i,j,k]之location

1. Row major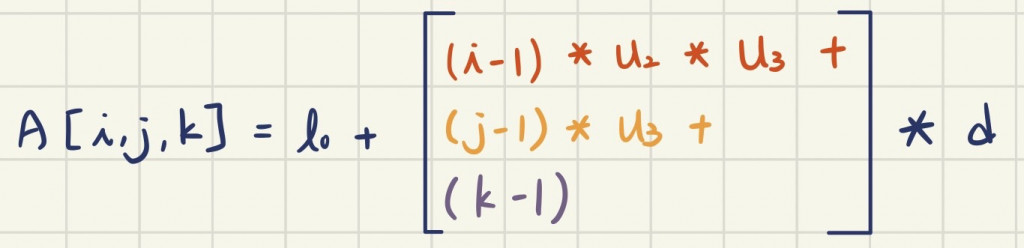
   

2. Column major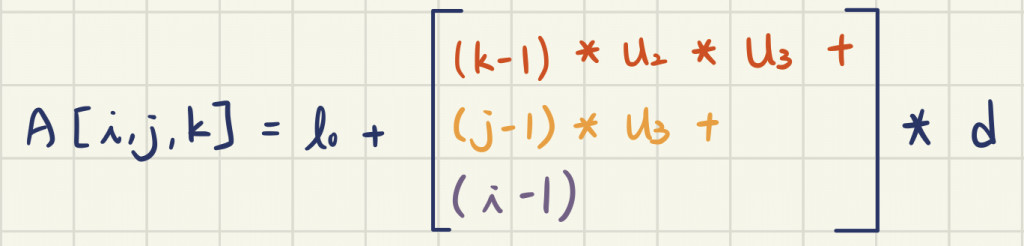
   

A[1..u₁,1..u₂,1..u₃,1..uₙ] of item
已知l₀,d
求A[i₁,i₂,i₃,...,iₙ]之location

1. Row major
   

2. Column major