上回講完了深度優先搜尋以及廣度優先搜尋的概念了，但想必有些人對於他到底是怎麼樣運作的還是有些不清楚。我們這回就利用leetcode上的習題來實際應用這兩種演算法，讓大家能夠更清楚的理解。

深度優先學習(DFS) -- 後續遍歷

145. Binary Tree Postorder Traversal
     Given the root of a binary tree, return the postorder traversal of its nodes' values.
     
     以上為題目概述，若想更加清楚了解題目，可以前往題目來源網站。
     https://leetcode.com/problems/binary-tree-postorder-traversal/

這道題目要我們所做的就是二元樹的後序遍歷，也就是利用深度優先搜尋的概念，獲得closed list的節點順序。那我的解題思維是先做第一層判斷，我們的根結點是否存在，若不存在則直接回傳空的list。排除這項可能過後，我們便可以開始使用深度優先搜尋來解題了。由於這道題是二元樹的遍歷，因此我們在確認展開的可能節點時就只需要先確認是否有左子節點，再確認是否有右子節點，如此以遞迴的形式完成二元樹的遍歷。

程式設計如下：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        if (root == None):
            return []
        result = []
        def dfs(node):
            if (node.left != None):
                dfs(node.left)
            if (node.right != None):
                dfs(node.right)
            result.append(node.val)
        dfs(root)
        return result

廣度優先搜尋(BFS) -- 層序遍歷

102. Binary Tree Level Order Traversal
     Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).
     
     
     以上為題目概述，若想更加清楚了解題目，可以前往題目來源網站。
     https://leetcode.com/problems/binary-tree-level-order-traversal/

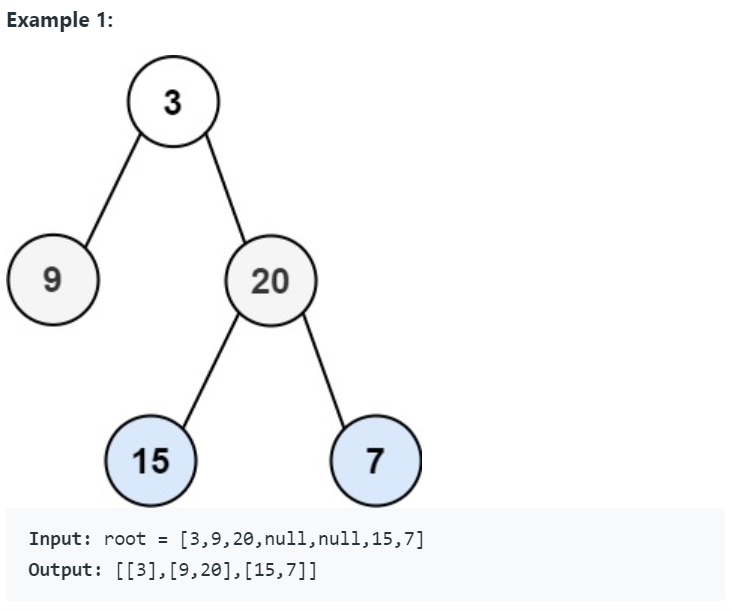
這道題要我們做的是二元樹的層序遍歷，也就是用廣度優先搜尋去獲得closed list中各層展開的情形。那我的解題思維是一樣先做第一層判斷根節點是否存在，若不存在則直接回傳空的list。去除掉這個例外後便開始利用廣度優先搜尋做節點的展開，先將根節點放至open list之中，接著展開所有可能後將節點放進closed list，並將所有的展開節點放進open list，反覆循環就能夠將每一層的遍歷給做完了。

程式設計如下：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if (root == None):
            return []
        
        def bfs():
            result.append([])
            for node in queue:
                if (node.left != None):
                    temp.append(node.left)
                    result[-1].append(node.left.val)
                if (node.right != None):
                    temp.append(node.right)
                    result[-1].append(node.right.val)
        
        queue = [root]
        temp = []
        result = [[root.val]]
        while (len(queue) != 0):
            bfs()
            queue = temp
            temp = []
        
        result.pop()
        return result