Clone Graph

Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

Test case format:

For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.

An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

Examples

Example 1:

Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Constraints:

• The number of nodes in the graph is in the range [0, 100].
• 1 <= Node.val <= 100
• Node.val is unique for each node.
• There are no repeated edges and no self-loops in the graph.
• The Graph is connected and all nodes can be visited starting from the given node

解析

一個資料結構 Node 裏面紀錄了該點的值 Val 還有透過陣列 Neighbor 來紀錄相連的 Node 參造 如下

  class Node {
    public int val;
    public List<Node> neighbors;
}

透過這種結構可以紀錄一個連結的 Graph

題目給定了一個 Graph 的起始 Node 參造

要求寫一個演算法來把這個 Graph 結構複製

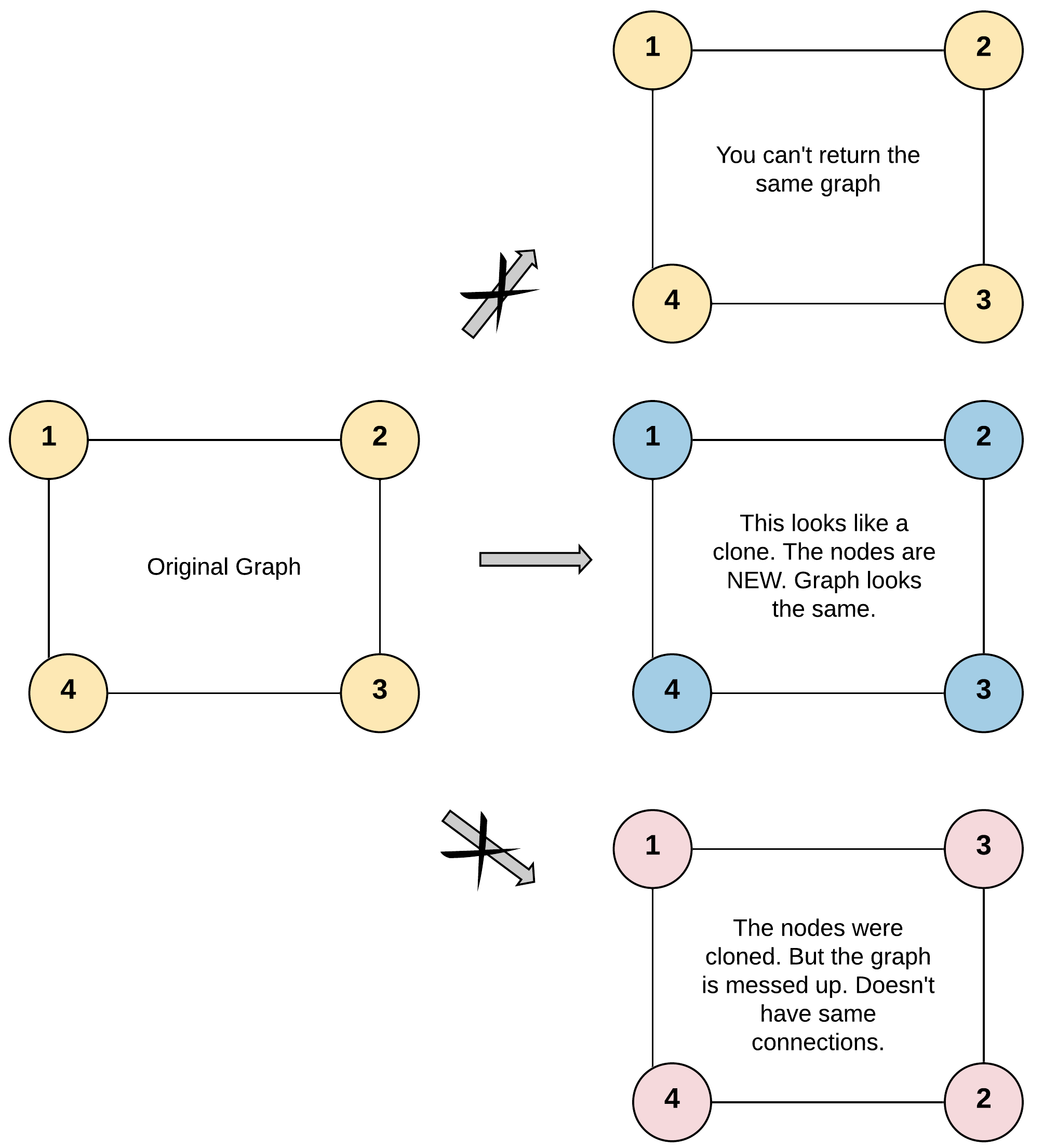
直覺的作法是從最開始的點透過 BFS 逐個複製

特別要注意的是因為是無向連結，所以必須標注已經走過的結點，避免重複拜訪已走過的 neighbor

如下圖

第2種作法是透過 DFS

每次先建立當下的 copyNode 然後把新舊對應的透過 hashmap 紀錄下來

然後當作完一輪後原本的 reference 就會自動建立好了

程式碼

package sol

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Neighbors []*Node
 * }
 */

func cloneGraph(node *Node) *Node {
	if node == nil {
		return nil
	}
	visit := make(map[int]*Node)
	created := make(map[int]*Node)
	var result *Node
	var bfs = func(node *Node) {
		queue := []*Node{node}
		for len(queue) != 0 {
			top := queue[0]
			queue = queue[1:]
			// mark as visited
			visit[top.Val] = top
			// create top if no existed
			var cur *Node
			if found, ok := created[top.Val]; ok {
				cur = found
			} else {
				cur = &Node{Val: top.Val}
				created[cur.Val] = cur
			}
			// assign to result if cur.Val = 1
			if cur.Val == 1 {
				result = cur
			}
			// copy Neighbors if exists
			nLen := len(top.Neighbors)
			if nLen != 0 {
				cur.Neighbors = make([]*Node, nLen)
				for idx := range top.Neighbors {
					n := top.Neighbors[idx]
					var newNode *Node
					if find, ok := created[n.Val]; ok {
						newNode = find
					} else {
						newNode = &Node{Val: n.Val}
						created[n.Val] = newNode
					}
					cur.Neighbors[idx] = newNode
					// check if not visited push to queue
					if _, ok := visit[n.Val]; !ok {
						queue = append(queue, n)
					}
				}
			}
		}
	}
	bfs(node)
	return result
}
/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Neighbors []*Node
 * }
 */

func cloneGraphDFS(node *Node) *Node {
	if node == nil {
		return nil
	}
	oldToNew := make(map[*Node]*Node)
	var dfs func(node *Node) *Node
	dfs = func(node *Node) *Node {
		if found, ok := oldToNew[node]; ok {
			return found
		}
		newNode := &Node{Val: node.Val}
		oldToNew[node] = newNode
		for _, nei := range node.Neighbors {
			newNode.Neighbors = append(newNode.Neighbors, dfs(nei))
		}
		return newNode
	}
	return dfs(node)
}

困難點

1. 需要知道如何透過 neighbor 結構往下迭代到所有結點
2. 需要防止把建立過的結點重複建立
3. 需要避免重複走入走過的結點

Solve Point

• [x] Understand what problem to solve
• [x] Analysis Complexity