昨天講了利用array來儲存一維,二維,三維....到n維矩陣，今天繼續來用array，我們來儲存一些酷逼八的矩陣(♛‿♛)

下、上三角矩陣

下三角矩陣(Lower-Triangular Matrix)

(一)定義:令A為n*n方陣，且對角線(不含)右上方元素均為0，其餘為其他元素
即A[i,j]=0 ,if i<j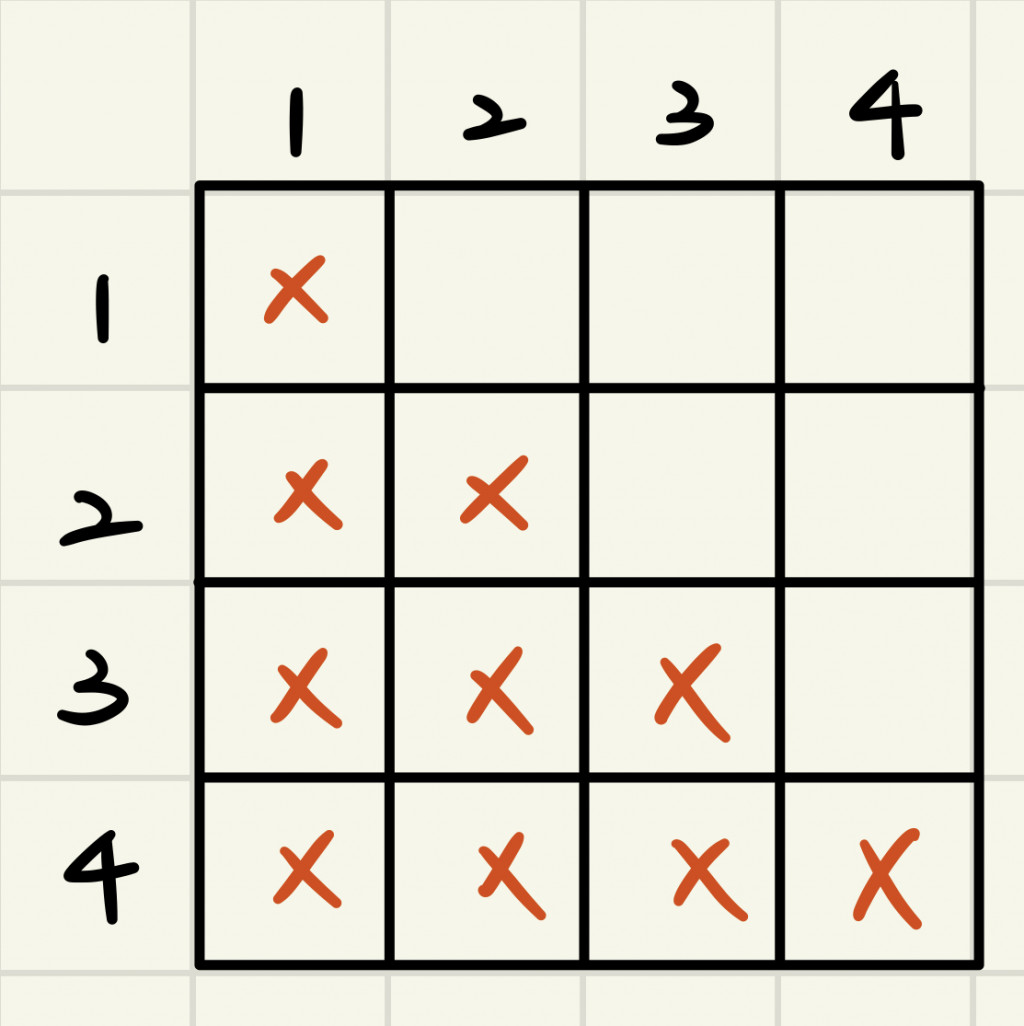

(二)元素個數=1+2+3+...+n=(n+1)n/2
(三)為了節省儲存空間，通常不會用 n*n array 去存放，而是使用B:array[1..(n+1)*n/2]去存放A[i,j]的i≥j之元素，將A[i,j]元素存入B[k]之公式分為兩種:

• Row major
  k = [1+2+3+...+(i-1)] + j = i(i-1)/2+j
  前面(i-1)列元素個數+第i列上的第幾個
• Column major
  k = n(j-1)-[0+1+2+...+(j-2)] + i-j+1
  前面(j-1)行元素個數+第j行上的第幾個
  = n(j-1)-[0+1+2+...+(j-2)+(j-1)] + i
  = n(j-1) - j(j-1)/2 + i

上三角矩陣(Upper-Triangular Matrix)

(一)定義:令A為n*n方陣，且對角線(不含)左下方元素均為0，其餘為其他元素
即A[i,j]=0 ,if i>j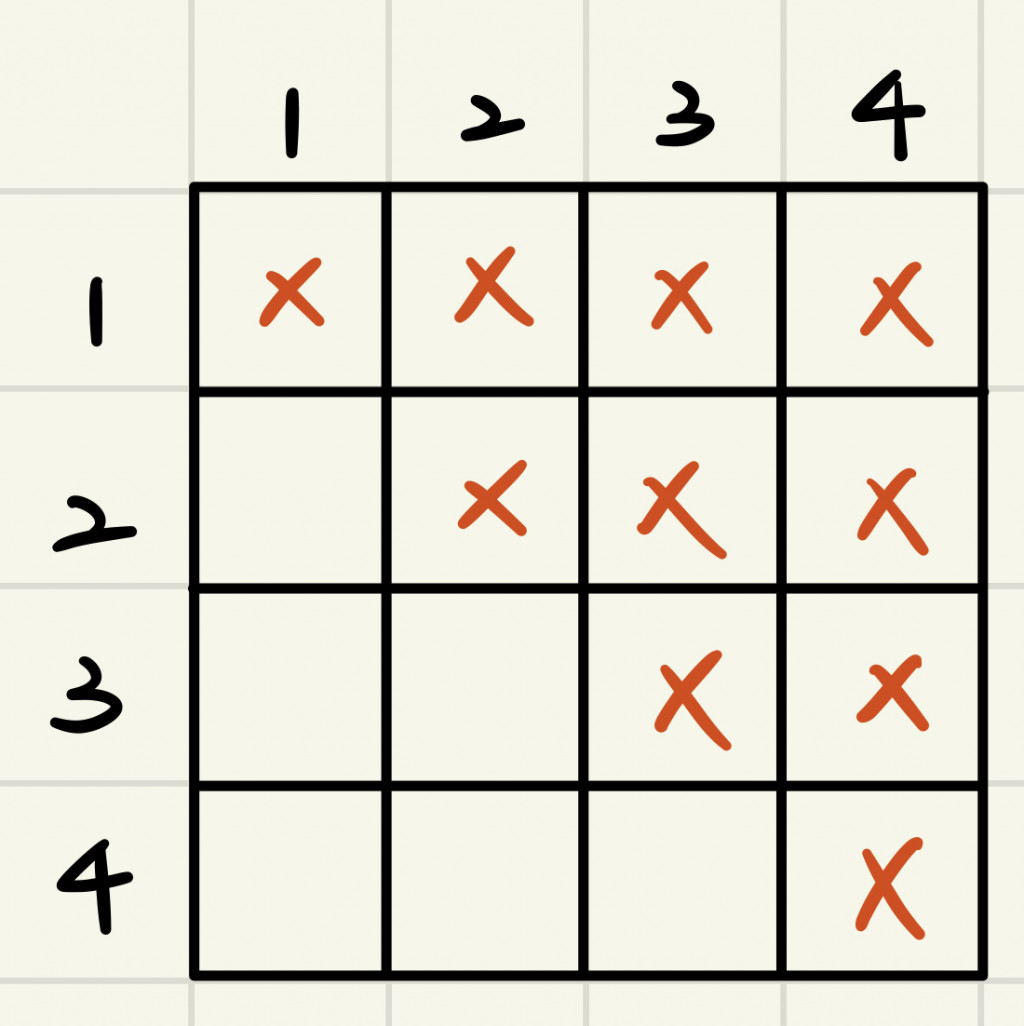

(二)元素個數=1+2+3+...+n=(n+1)*n/2
(三)使用B:array[1..(n+1)*n/2]去存放A[i,j]的i≥j之元素，將A[i,j]元素存入B[k]之公式分為兩種:

• Column major
  k = [1+2+3+...+(j-1)] + i = j(j-1)/2+i
  前面(j-1)行元素個數+第J行上的第幾個

  Note:與下三角的Row major相似，只是i,j對調!!

• Row major
  k = n(i-1)-[0+1+2+...+(i-2)] + j-i+1
  前面(i-1)列元素個數+第i列上的第幾個
  = n(i-1)-[0+1+2+...+(i-2)+(i-1)] + j
  = n(i-1) - i(i-1)/2 + j

  Note:一樣與下三角的Column major相似，只是i,j對調!!

對稱矩陣(Symmetric Matrix)

(一)定義:令A為n*n方陣，且A[i,j]=A[j,i]

(二)對稱矩陣為了有效節省儲存空間，通常只需要存放下三角或上三角部分元素即可，所以只需要使用B[1..n(n+1)/2]來儲存，若我們希望此對稱矩陣放在B中呈現的順序是以上三角元素Column major方式，則將任一元素A[i,j]存入B[k]之公式為:
(可以使用MAX與min函數)

例如:A[1,3]存入B[k]，k=4 ; A[3,1]存入B[k]，k=4

1. 上三角元素，Column major順序
   所以A[i,j]，i≤j時，k=j(j-1)/2+i
2. 此一存放順序也等於是下三角的Row major順序
   所以A[i,j]，i≥j時，k=i(i-1)/2+j

合成兩式可以得到k = MAX(i,j)*[MAX(i,j)-1]/2 + min(i,j)

帶狀、寬帶矩陣(Band Matrix)

(一)定義:令Aₙ,ᵢ,ⱼ 代表Band Matrix，其中A是n*n方陣且對角線(含)左下i條斜線為元素，右上b條斜線為元素，其餘為0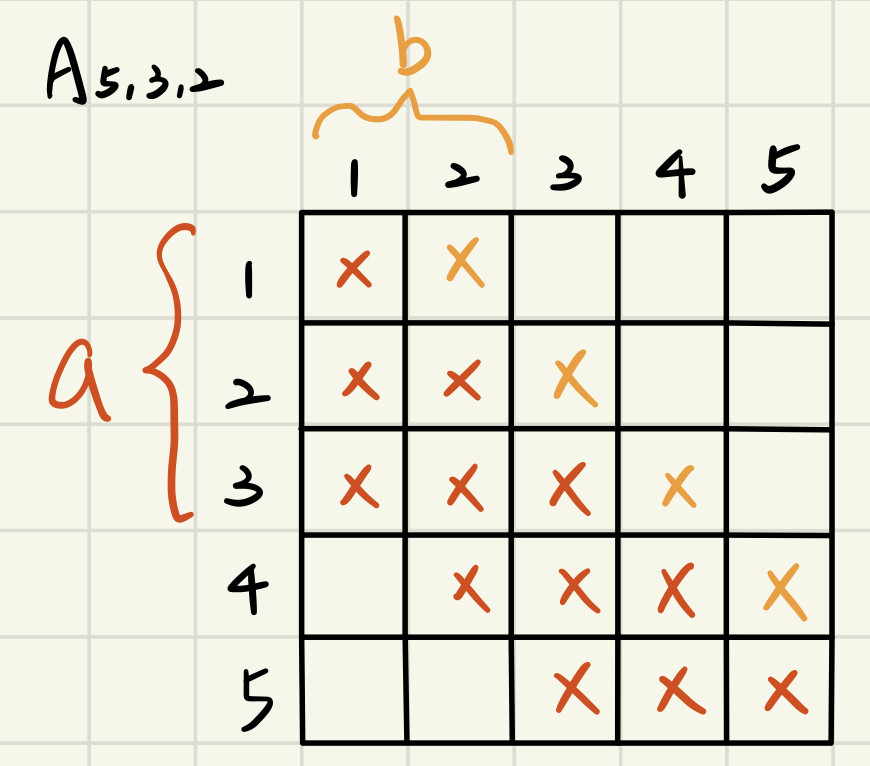

(二)Aₙ,ᵢ,ⱼ之元素個數

• a部分
  (n-a+1)+...+n = (2n-a+1)a/2

• b部分
  (n-b+1)+...+n = (2n-b+1)b/2

• 所以元素個數=(2n-a+1)a/2 + (2n-b+1)b/2 - n