Of course it is happening inside your head, Harry, but why on earth should that mean that it is not real?
-- Albus Dumbledore

A 4D skewb will be like

Definition: hyperskewb in general

I will try to convey my definition on hyperskewb, and why it makes sense in mathematical language at my best. It is beyond my ability to make them strictly formal, so they won't be. Maybe I should find some time to take advanced math classes...

Without loss of generality, we can assume the discussed hyperskewb is a n-dimension hypercub (with the axes being a_1, a_2, to a_n) being cut in a certain way. The value of the coordinates of the cube's vertices can only be either 1 or -1. In other words, the bounday of the hypercube is defined by all 2*n hyperplanes a_i = +/-1, where i is the integers from 1 to n. The center coordinates of this hyperskewb is thus at the origin.

Property 1: Deep-cut: The cut itself is a hyperplane that intersects with this hypercube. It passes origin and divides the hypercube into two isomorphic parts.

Assume the normal vector of an appropriate cut for hyperskewb is (k_1, k_2, ..., k_n). Then, the equation of the cut hyperplane must be

K = k_1*a_1 + k_2*a_2 + ... k_n*a_n = 0

because it should pass origin. The second sub-condition automatically holds for this equation, because for all point P (p_0, p_1, ..., p_n) inside this hypercube where

K(P) = k_1*p_1 + k_2*p_2 + ... k_n*p_n > 0, a point Q (-p_0, -p_1, ..., -p_n) must exist inside the cube and at the different side of the cut hyperplane, because K(Q) = -K(P) < 0. And vice versa.

Property 2: Vertex-turning

This definition can accept a very wide range of possible cuts, but non-regular cuts result in less symmetry.

We can choose all k_i being 1. Consider the smallest case where n=3, there are 6 special solutions to a_1 + a_2 + a_3 = 0 that cannot be represented as any two solutions' interpolation, which forms one of the cutting hexagons of a skewb. They are (-1, 0, 1), (-1, 1, 0), (0, -1, 1), (0, 1, -1), (1, -1, 0), (1, 0, -1).

For the hyperplane in higher dimensions, if n is odd, then there is exactly one 0 in the coordinates; it n is even, then there is no 0 in the coordinates. Both may seem unintuitive, so we can check a more relaxed statement: the coordinates of each vertice of the intersection (n-1)-polytope contains no more than 1 0s. By contradiction, from the two 0s, two more points can be derived by replacing them to (1,-1) and (-1,1), so that the original coordinates become a interpolation of the two derived points that also belong to the (n-1)-polytope (fit the equation) and the hypercube (all a_i are between -1 and 1).

Note that for all vertices, there can never be exactly one non-integer among all coordinate values; otherwise, the sum is obviously not possible to be zero. Also, a vertex has no non-integer coordinate value becase we can always choose any two non-integer coordinates, u and v and a small delta, such that replacing them with u+delta and v-delta pair or u-delta and v+delta pair still result in the intersection, and the u and v pair is a interpolation of the two points and thus cannot be a part of a vertex of the intersection. Therefore, the coordinate values of a vertex of the intersection between the cut hyperplane and the hypercube can only be integers (1, 0, or -1), and at most one 0 exists.

Let's finish the proof by contradiction. If n is odd and there is no 0 in a vertex's coordinate, then the sum of an odd numer of 1s and -1s will never be a 0; also, if n is even and there is one 0 in a vertex's coordinate, then the same situation emerges and cannot be possible, done.

It is easy to go one step further to calculate the number of vertices,

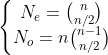
When n is 3, this gives us 6 (3 * C(3-1, 3/2) = 3 * C(2,1) = 6, a regular hexagon); when n is 4, which is what we are going into for the rest few days, it is interestingly also 6 (C(4, 2) = 6), and they forms a regular octahedron. We will go through this in more details tomorrow. If by the end of this series we still have time, I plan to investigate a little bit more about 5-skewb, whose cutting 4-polytope has 30 vertices but I don't know what it is yet. Also interestingly, 6-skewb's cutting 5-polytope has only 20 vertices. It does not form a monotonic increasing sequence.

Why is checking only a_1+a_2+...a_n=0 sufficient?

You may wonder why I mention only one cutting hyperplane while it ids the fact that there are many symmetrical cut makes the puzzles fun to play with. Yes, the keyword is symmetry. We showed that for 3-skewb yesterday. It has 8 vertices but the twists of half of them are equivalent. There are only 4 axes for a 3-skewb, and it can be generalized that n-skewb has 2^(n-1) axes, which means the same number of cutting hyperplanes.

The hyperplanes can be generated by reflectional symmetry. Their equations are merely tweaking the coefficients of a_is where i is larger than 1. The solutions that form a set of vertices are i-on-i and onto to the pure sum of all a_is.

Review: the idea of hyperskewb

When the idea of hyperskewb came to mind, I thought I was the first discoverer of this new types of puzzle. I didn't find it defined in MC4D or MagicTile or other few software I could try. Nor did Google return me anything related. With that excitement, I signed up for 14th ITHome Ironman, with this series Quest for Hyperskewb.

However, it is always near impossible to be a true first discoverer. Near the end of August, a few weeks after I signed up, I found some archived discussion dated back to 2011/01/23, titled "Other 4D Puzzles". In the thread, Galla Matthew shared the idea of the 4D puzzles, 4D FTO (Face-Turning Octahedron), 4D Skewb (!), and 4D Helicopter cube (a edge-turning shallower-than-origin-cut 12-axis jumble-able puzzle). The last two are interesting as well, but let's focus on skewb-related stuff now.

A few weeks ago when I started to prepare the materials, I recalled this thread and went ask the community if there was any realization to the 4D skewb. It turns out the Magic Puzzle Ultimate very likely include this puzzle. I cannot be 100% sure because I didn't run it myself (it supports Windows only while I don't have any windows machine for a long time), but there is related snapshots. Anyway, even if it is not by default supported, the configuration framework of MPUlt allows the generation of the puzzle.

Other than 4D, there is a CT entry for 5D hypercube in MPUlt, and was solved in 2013 by the author of the software, Andrey Astrelin, himeself. If CT means corner-turning, then it matches my definition to 5D skewb as well.

After I scan over the MPUlt source, I realize that I need more study to understand the legacy, but it is beyond the scope of this series.

Conclusion

It's amazing we already came this far. After all the fundamentals, 2x2x2x2, skewb, we are finally here. It's a shame that I am a little bit late to the party, but that's OK. I will keep finishing this series as my quest.

小結

在笛卡爾座標系中簡單證明高維 skewb 的性質。